题目内容
11. 如图所示,AB为一光滑水平横杆,杆上套一质量为M的小圆环,环上系一长为L质量不计的细绳,绳的另一端拴一质量为m的小球,现将绳拉直,且与AB平行,由静止释放小球,则:
如图所示,AB为一光滑水平横杆,杆上套一质量为M的小圆环,环上系一长为L质量不计的细绳,绳的另一端拴一质量为m的小球,现将绳拉直,且与AB平行,由静止释放小球,则:(1)当线绳与AB成θ角时,圆环移动的距离是多少?
(2)求小球运动到最低点时的速度大小.
分析 (1)在小球向下摆动的过程中,虽然小球、细绳及圆环在运动过程中合外力不为零(杆的支持力与两圆环及小球的重力之和不相等),系统的动量不守恒,但是系统在水平方向不受外力,因而水平动量守恒.用位移与时间之比表示速度,根据水平方向动量守恒和几何关系列式求解.
(2)根据系统水平方向的动量守恒和机械能守恒分别列式,联立可求小球运动到最低点时的速度大小.
解答 解:(1)虽然小球、细绳及圆环在运动过程中合外力不为零(杆的支持力与两圆环及小球的重力之和不相等),系统动量不守恒,但是系统在水平方向不受外力,因而水平动量守恒.设细绳与AB成θ角时小球的水平速度为v,圆环的水平速度为V,取水平向右为正方向,由水平动量守恒有:
MV-mv=0
且在任意时刻或位置V与v均满足这一关系,加之时间相同,公式中的V和v可分别用其水平位移替代,则上式可写为:
Md-m[(L-Lcosθ)-d]=0
解得圆环移动的距离:d=$\frac{mL(1-cosθ)}{M+m}$
(2)设小球运动到最低点时,圆环和小球的速度大小分别为v1和v2.根据系统水平方向动量守恒和机械能守恒得:
0=Mv1+mv2;
mgL=$\frac{1}{2}$Mv12+$\frac{1}{2}$mv22;
联立解得:v2=$\sqrt{\frac{2MgL}{m+M}}$
答:(1)当线绳与AB成θ角时,圆环移动的距离是$\frac{mL(1-cosθ)}{M+m}$.
(2)小球运动到最低点时的速度大小是$\sqrt{\frac{2MgL}{m+M}}$.
点评 解决本题的关键要明确系统水平方向的动量守恒,能用位移表示出速度,不过要注意位移的参考系必须是地面.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
2.一名静止的相扑运动员甲和一名正在跑道上高速奔跑的短跑运动员乙相比较( )
| A. | 由于甲静止,乙高速运动,甲的惯性小,乙的惯性大 | |
| B. | 由于甲、乙的运动状态不同,甲、乙的惯性大小无法比较 | |
| C. | 由于甲的质量比乙的质量大,甲的惯性比乙的惯性大 | |
| D. | 由于甲静止,乙高速运动,甲无惯性,乙具有惯性 |
19. 甲、乙两质点从同一位置出发,沿同一直线路面运动,它们的v-t图象如图所示.对这两质点在0~3s内运动的描述,下列说法正确的是( )
甲、乙两质点从同一位置出发,沿同一直线路面运动,它们的v-t图象如图所示.对这两质点在0~3s内运动的描述,下列说法正确的是( )
 甲、乙两质点从同一位置出发,沿同一直线路面运动,它们的v-t图象如图所示.对这两质点在0~3s内运动的描述,下列说法正确的是( )
甲、乙两质点从同一位置出发,沿同一直线路面运动,它们的v-t图象如图所示.对这两质点在0~3s内运动的描述,下列说法正确的是( )| A. | t=2 s时,甲、乙两质点相遇 | |
| B. | 在甲、乙两质点相遇前,t=1 s时,甲、乙两质点相距最远 | |
| C. | 甲质点的加速度比乙质点的加速度小 | |
| D. | t=3 s时,乙质点在甲质点的前面 |
6.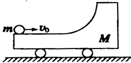 带有$\frac{1}{4}$光滑圆弧轨道,质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回并脱离滑车时,以下说法正确的是( )
带有$\frac{1}{4}$光滑圆弧轨道,质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回并脱离滑车时,以下说法正确的是( )
 带有$\frac{1}{4}$光滑圆弧轨道,质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回并脱离滑车时,以下说法正确的是( )
带有$\frac{1}{4}$光滑圆弧轨道,质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回并脱离滑车时,以下说法正确的是( )| A. | 小球一定水平向左做平抛运动 | B. | 小球可能水平向左做平抛运动 | ||
| C. | 小球不可能做自由落体运动 | D. | 小球不可能水平向右做平抛运动 |
16.下面关于电势和电势能的说法正确的是( )
| A. | 同一电荷,在电势高处比在电势低处具有的电势能多 | |
| B. | 在正电荷形成的电场中的某点,正电荷所具有的电势能,多于负电荷在同一点所具有的电势能 | |
| C. | 正电荷自电势越高的地方,所具有的电势能越多,负电荷处在电势越低的地方电势能越少 | |
| D. | 放在电场中某一定点的正电荷,其电量越多,具有的电势能不一定越多 |
3. 如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )
如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )
 如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )
如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )| A. | 外力F=mgtan2θ | |
| B. | 外力F=mgtanθ | |
| C. | 当物块沿斜面向上匀速滑行时,地面对斜面有向左的静摩擦力 | |
| D. | 当物块沿斜面向下匀速滑行时,斜面受到5个力作用 |
1.根据相对论,下列说法正确的是( )
| A. | 在不同的惯性参考系中,物理定律的数学形式是不同的 | |
| B. | 真空中的光速在不同惯性参考系中不相同的 | |
| C. | 一条沿身长度方向高速运动的杆子,其长度与静止时不同 | |
| D. | 一条沿垂直于自身长度的方向高速运动杆子,其长度与静止时不同 |


 在真空中的O点放一个Q=1×10-9 C的点电荷,直线MN过O点,OM=30cm,M点放有一个q=-1×10-10C的点电荷,如图所示,求:
在真空中的O点放一个Q=1×10-9 C的点电荷,直线MN过O点,OM=30cm,M点放有一个q=-1×10-10C的点电荷,如图所示,求: