题目内容
如图所示, ab、ef是平行地固定在水平绝缘桌面上的光滑金属导轨,导轨间距为d.在导轨左端a、c上连有一个阻值为R的电阻,一质量为3m,长为d的金属棒恰能置于导轨上并和导轨良好接触。起初金属棒静止于MN位置,整个装置处于方向垂直桌面向下、磁感应强度为B的磁场中。现有一质量为m的带电量为q的绝缘小球在桌面上从O点(O为导轨上的一点)以与ef成60°斜向右方射向ab,随后小球直接垂直地打在金属棒的中点上,并和棒粘合在一起(设小球与棒之间没有电荷转移)。小球运动过程中不计导轨间电场的影响,导轨和金属棒的电阻不计。求:
(1)小球射入磁场时的初速度υ0;
(2)电阻R上产生的总热量Q
(3)通过电阻R的总电量Δq.

(1)![]() (2)
(2)![]() (3)
(3)![]()
解析:
⑴小球入射磁场后将作匀速圆周运动,设圆周运动的半径为r,其轨迹如图所示(略)
由几何知识可知:![]() (3分)
(3分)
解得 ![]() ① (2分)
① (2分)
小球在磁场中作圆周运动: ![]() ② (2分)
② (2分)
由①、②得: ![]() ③ (1分)
③ (1分)
⑵小球和金属棒的碰撞过程,由动量守恒定律得:
mυ0=(m+3m)υ ④ (2分)
金属棒切割磁感线的过程中,棒和小球的动能转化为电能进而转化成焦耳热:
![]() ⑤ (2分)
⑤ (2分)
由③、④、⑤可得: ![]() ⑥ (2分)
⑥ (2分)
棒和小球的速度从υ1变为0的过程中由动量定理有:
![]() ⑦ (1分) 又
⑦ (1分) 又![]() ⑧ (4分)
⑧ (4分)
由③、④、⑦、⑧可得 ![]() ⑨ (2分)
⑨ (2分)

 阅读快车系列答案
阅读快车系列答案 如图所示,电源电动势E=6V,电源内阻不计.定值电阻R1=2.4kΩ、R2=4.8kΩ.
如图所示,电源电动势E=6V,电源内阻不计.定值电阻R1=2.4kΩ、R2=4.8kΩ. 如图所示,AB、CD为光滑水平轨道,DE是半径为R1=0.3m的
如图所示,AB、CD为光滑水平轨道,DE是半径为R1=0.3m的 如图所示,AB是一段位于竖直平面内的弧形轨道,高度为h,末端B处的切线沿水平方向.一个质量为m的小物体P(可视为质点)从轨道顶端处A点由静止释放,滑到B点时以水平速度v飞出,落在水平地面的C点,其轨迹如图中虚线BC所示.已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不计空气阻力的作用.
如图所示,AB是一段位于竖直平面内的弧形轨道,高度为h,末端B处的切线沿水平方向.一个质量为m的小物体P(可视为质点)从轨道顶端处A点由静止释放,滑到B点时以水平速度v飞出,落在水平地面的C点,其轨迹如图中虚线BC所示.已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不计空气阻力的作用. (2008?滨州二模)单匝矩形线圈abcd放在匀强磁场中,如图所示,ab=de=l1,ad=bc=l2,从图示位置起以角速度ω绕不同转轴做匀速转动,则( )
(2008?滨州二模)单匝矩形线圈abcd放在匀强磁场中,如图所示,ab=de=l1,ad=bc=l2,从图示位置起以角速度ω绕不同转轴做匀速转动,则( )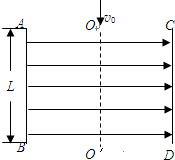 如图所示,AB、CD两金属板间形成一匀强电场(板的边缘电场不考虑),板长为L,电场强度为E.一质量为m,电荷量为+q的粒子(不计重力)沿两板的中间线OO′从AC中点O处以初速度v0射入匀强电场,粒子恰好能从极板边缘上的D点射出匀强电场.求:
如图所示,AB、CD两金属板间形成一匀强电场(板的边缘电场不考虑),板长为L,电场强度为E.一质量为m,电荷量为+q的粒子(不计重力)沿两板的中间线OO′从AC中点O处以初速度v0射入匀强电场,粒子恰好能从极板边缘上的D点射出匀强电场.求: