题目内容
3. 如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软丝绸.丝绸恰好将两侧斜面覆盖,现将质量为mA的A物体和质量为mB的B物体轻放在斜面,如图在示的位置开始计时,斜面长度及斜面倾角图中已标出,两物体可视为质点.若mA=3kg,mB=lkg,A与丝绸间的动摩擦因数μA=$\frac{1}{3}$,B与丝绸间的动摩擦因数μB=$\frac{4}{5}$,假设两物体与丝绸间的滑动摩擦力与最大静摩擦力相等,试求从计时开始,A、B两物体到达斜面底端所用时间分别为多少.(sin37°=0.6,cos37°=0.8,g取10m/s2)
如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软丝绸.丝绸恰好将两侧斜面覆盖,现将质量为mA的A物体和质量为mB的B物体轻放在斜面,如图在示的位置开始计时,斜面长度及斜面倾角图中已标出,两物体可视为质点.若mA=3kg,mB=lkg,A与丝绸间的动摩擦因数μA=$\frac{1}{3}$,B与丝绸间的动摩擦因数μB=$\frac{4}{5}$,假设两物体与丝绸间的滑动摩擦力与最大静摩擦力相等,试求从计时开始,A、B两物体到达斜面底端所用时间分别为多少.(sin37°=0.6,cos37°=0.8,g取10m/s2)
分析 先假设纸带不动,判断出物体A和B的受力情况;然后得到物体A和B的实际运动情况,然后结合牛顿第二定律和运动学公式列式求解.
解答 解:先假设绸带固定不动,再把物体A、B按题中条件放置在斜面上
对A物体受力分析计算得:mAgsin53°=3×10×0.8=24N>μAmAgcos53°=$\frac{1}{3}$×3×10×0.6=6N,则A相对绸带滑动;
对B物体受力分析计算得:mBgsin37°=1×10×0.6=6N<μBmBgcos37°=0.8×1×10×0.8=6.4N,则B相对绸带不滑动;
对B和绸带整体分析,A对绸带滑动摩擦力f=μAmAgcos53°=6N,B物体沿斜面分力mBgsin37°=6N
则说明若A、B和绸带同时释放后,B和绸带先静止不动,A沿绸带加速下滑3m后,B再拖动绸带一起沿光滑斜面加速下滑.
A沿绸带下滑过程中:
mAgsin53°-μAmAgcos53°=mAa1
解得:a1=gsin53°-μAgcos53°=10×0.8-$\frac{1}{3}$×10×0.6=6m/s2
根据位移时间公式,有x1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$,
代入数据解得t1=1s
B拖动绸带一起沿光滑斜面加速下滑过程中:
mBgsin37°=mBa2
代入数据解得:a2=gsin37°=10×0.6=6m/s2
根据位移时间公式,有x2=$\frac{1}{2}{a}_{2}{t}_{2}^{2}$,解得t2=1s
则从开始计时的时间t=t1+t2=2s
答:从计时开始,A到达斜面底端的时间1s,B到过斜面底端的时间2s.
点评 本题关键是灵活选择研究对象,通过受力分析,确定物体的运动规律,最后结合运动学公式列式求解出物体的运动学参量.

| A. | 温度高的物体内能不一定大,但分子平均动能一定大 | |
| B. | 雨伞伞面上有许多细小的孔,却能遮雨,是因为水的表面张力作用 | |
| C. | 橡胶无固定的熔点,是非晶体 | |
| D. | 热机的效率可以100% | |
| E. | 气体很容易充满整个容器,这是分子间存在斥力的宏观表现 |
 2015年莫斯科世锦赛上,我国男子短道速滑队时隔15年再次站到5000m接力的冠军领奖台上.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲,甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )
2015年莫斯科世锦赛上,我国男子短道速滑队时隔15年再次站到5000m接力的冠军领奖台上.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲,甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )| A. | 甲对乙的作用力与乙对甲的作用力相同 | |
| B. | 甲对乙的作用力一定做正功,乙的动能增大 | |
| C. | 乙对甲的作用力一定做正功,甲的动能增大 | |
| D. | 甲的动能增加量一定等于乙的动能减少量 |
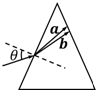 在玻璃中有一个截面为三角形的柱状真空空腔,a、b两束单色光以同样的入射角θ由玻璃射入空腔,部分光路如图,下列说法正确的是( )
在玻璃中有一个截面为三角形的柱状真空空腔,a、b两束单色光以同样的入射角θ由玻璃射入空腔,部分光路如图,下列说法正确的是( )| A. | 若增大θ,b光在空腔内先消失 | |
| B. | 若改变θ,a光通过空腔的时间一定比b光短 | |
| C. | 在同一双缝干涉装置上的干涉条纹a光较宽 | |
| D. | 若将两个相同的小球分别涂上a、b两种颜色放在同样深度的水中,在水面上看涂a颜色的小球较浅 |
 现代观测表明,由于引力作用,恒星有“聚集”的特点,众多的恒星组成了不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星,事实上,冥王星也是和另一星体构成双星,如图所示,这两颗行星m1、m2各以一定速率绕它们连线上某一中心O匀速转动,这样才不至于因万有引力作用而吸引在一起,现测出双星间的距离始终为L,且它们做匀速圆周运动的半径r1与r2之比为3:2,则( )
现代观测表明,由于引力作用,恒星有“聚集”的特点,众多的恒星组成了不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星,事实上,冥王星也是和另一星体构成双星,如图所示,这两颗行星m1、m2各以一定速率绕它们连线上某一中心O匀速转动,这样才不至于因万有引力作用而吸引在一起,现测出双星间的距离始终为L,且它们做匀速圆周运动的半径r1与r2之比为3:2,则( )| A. | 它们的角速度大小之比为2:3 | B. | 它们的线速度大小之比为3:2 | ||
| C. | 它们的质量之比为3:2 | D. | 它们的周期之比为2:3 |
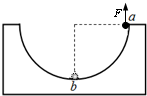 如图所示,一光滑小球在力F的作用下,以某一恒定的速率,从半径为R的固定的半圆形轨道的a点沿轨道运动到b点,作用力F的方向总是竖直向上.空气阻力不计,下面关于小球在该过程中的有关说法正确的是( )
如图所示,一光滑小球在力F的作用下,以某一恒定的速率,从半径为R的固定的半圆形轨道的a点沿轨道运动到b点,作用力F的方向总是竖直向上.空气阻力不计,下面关于小球在该过程中的有关说法正确的是( )| A. | 加速度恒定不变 | B. | 所受合外力恒定不变 | ||
| C. | 轨道的弹力不断增大 | D. | F与重力的合力恒定不变 |
 如图,水平面内有一光滑金属导轨,其MN、PQ边的电阻不计,MP边的电阻阻值R=1Ω,MN与MP的夹角为127°,PQ与MP垂直,MP边长度等于1m.将质量m=2kg,电阻不计的足够长直导体棒搁在导轨上,并与MP平行.棒与MN、PQ交点G、H间的距离L1=5m,E、F间的距离L2=2m.空间存在垂直于导轨平面的匀强磁场,磁感应强度B=0.1T.在外力作用下,棒由GH处以一定的初速度向左做直线运动,运动时回路中的电流强度始终与初始时的电流强度相等.(sin37°=0.6;cos37°=0.8)
如图,水平面内有一光滑金属导轨,其MN、PQ边的电阻不计,MP边的电阻阻值R=1Ω,MN与MP的夹角为127°,PQ与MP垂直,MP边长度等于1m.将质量m=2kg,电阻不计的足够长直导体棒搁在导轨上,并与MP平行.棒与MN、PQ交点G、H间的距离L1=5m,E、F间的距离L2=2m.空间存在垂直于导轨平面的匀强磁场,磁感应强度B=0.1T.在外力作用下,棒由GH处以一定的初速度向左做直线运动,运动时回路中的电流强度始终与初始时的电流强度相等.(sin37°=0.6;cos37°=0.8) 如图所示,一半径为R圆心角为240°的扇形单匝线圈可绕着磁场的边界线上的O点以逆时针方向转动,角速度为ω,磁场的磁感应强度为B.则从图示位置开始计时,能正确反映线圈中感应电动势随时间变化的关系图象是(以逆时针方向为电流的正向)( )
如图所示,一半径为R圆心角为240°的扇形单匝线圈可绕着磁场的边界线上的O点以逆时针方向转动,角速度为ω,磁场的磁感应强度为B.则从图示位置开始计时,能正确反映线圈中感应电动势随时间变化的关系图象是(以逆时针方向为电流的正向)( )


