题目内容
11.警察发现前方100m处有一超载汽车正以15m/s的速度匀速前进,这时警车立即从静止出发,若警车要在20s内追上超载汽车.则:(1)警车至少以多大的加速度追赶汽车?
(2)若警车以最小的加速度追赶,追上之前与超载汽车最远相距多少?
分析 根据位移关系,结合位移时间公式求出追及的加速度大小.
当两者的速度相等时,相距最远,结合速度时间公式求出速度相等的时间,根据位移公式求出相距的最远距离.
解答 解:(1)设警车的最小加速度为a,则有:
$vt+100=\frac{1}{2}a{t}^{2}$,
代入数据得:15×20+100=$\frac{1}{2}×a×400$
解得:a=2m/s2.
(2)两车速度相等的时间为:$t′=\frac{v}{a}=\frac{15}{2}s=7.5s$,
此时汽车的位移为:x1=vt′=15×7.5m=112.5m,
警车的位移为:${x}_{2}=\frac{1}{2}at{′}^{2}=\frac{1}{2}×2×7.{5}^{2}m$=56.25m,
则相距的最远距离为:△x=x1+100-x2=112.5+100-56.25m=156.25m.
答:(1)警车至少以2m/s2的加速度追赶汽车.
(2)若警车以最小的加速度追赶,追上之前与超载汽车最远相距为156.25m.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时两者的位移最大.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
1. 一带电粒子沿图中AB曲线穿过匀强电场中的一组等势面,等势面的电势关系满足φa>φb>φc>φd.若不计粒子所受重力,则( )
一带电粒子沿图中AB曲线穿过匀强电场中的一组等势面,等势面的电势关系满足φa>φb>φc>φd.若不计粒子所受重力,则( )
 一带电粒子沿图中AB曲线穿过匀强电场中的一组等势面,等势面的电势关系满足φa>φb>φc>φd.若不计粒子所受重力,则( )
一带电粒子沿图中AB曲线穿过匀强电场中的一组等势面,等势面的电势关系满足φa>φb>φc>φd.若不计粒子所受重力,则( )| A. | 粒子一定带正电 | |
| B. | 粒子的运动是匀变速曲线运动 | |
| C. | 粒子从A点到B点运动过程中电势能增加 | |
| D. | 粒子从A点到B点运动过程中动能先减少后增大 |
6. 如图所示,两个同心金属环水平放置,半径分别为r和2r,两环间有磁感应强度大小为B、方向垂直环面向里的匀强磁场,在两环间连接有一个电容为C的电容器,a、b是电容器的两个极板.长为r的金属棒AB沿半径方向放置在两环间且与两环接触良好,并绕圆心以角速度ω做逆时针方向(从垂直环面向里看)的匀速圆周运动,则下列说法正确的是( )
如图所示,两个同心金属环水平放置,半径分别为r和2r,两环间有磁感应强度大小为B、方向垂直环面向里的匀强磁场,在两环间连接有一个电容为C的电容器,a、b是电容器的两个极板.长为r的金属棒AB沿半径方向放置在两环间且与两环接触良好,并绕圆心以角速度ω做逆时针方向(从垂直环面向里看)的匀速圆周运动,则下列说法正确的是( )
 如图所示,两个同心金属环水平放置,半径分别为r和2r,两环间有磁感应强度大小为B、方向垂直环面向里的匀强磁场,在两环间连接有一个电容为C的电容器,a、b是电容器的两个极板.长为r的金属棒AB沿半径方向放置在两环间且与两环接触良好,并绕圆心以角速度ω做逆时针方向(从垂直环面向里看)的匀速圆周运动,则下列说法正确的是( )
如图所示,两个同心金属环水平放置,半径分别为r和2r,两环间有磁感应强度大小为B、方向垂直环面向里的匀强磁场,在两环间连接有一个电容为C的电容器,a、b是电容器的两个极板.长为r的金属棒AB沿半径方向放置在两环间且与两环接触良好,并绕圆心以角速度ω做逆时针方向(从垂直环面向里看)的匀速圆周运动,则下列说法正确的是( )| A. | 金属棒中有从A到B的电流 | B. | 电容器a极板带正电 | ||
| C. | 电容器所带电荷量为$\frac{3CBω{r}^{2}}{2}$ | D. | 电容器所带电荷量为$\frac{CBω{r}^{2}}{2}$ |
3. 如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从圆环中穿过且不与圆环接触,下列说法正确的是( )
如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从圆环中穿过且不与圆环接触,下列说法正确的是( )
 如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从圆环中穿过且不与圆环接触,下列说法正确的是( )
如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从圆环中穿过且不与圆环接触,下列说法正确的是( )| A. | 圆环中感应电流的方向(从上向下看),先顺时针后逆时针 | |
| B. | 圆环中感应电流的方向(从上向下看),先逆时针后顺时针 | |
| C. | 条形磁铁在下落过程中的加速度始终大于重力加速度g | |
| D. | 条形磁铁在下落过程中动能的增加量等于其重力势能的减少量 |
20.A、B两个物体在同一直线上运动,它们的速度图象如图所示,则( )
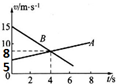

| A. | 在0至4s内A、B两物体运动方向相反 | |
| B. | 在4S时A、B两物体相遇 | |
| C. | t=4s时,A、B两物体的速度大小相等,方向相同 | |
| D. | A做匀加速直线运动,B做匀减速直线运动 |
1.一台理想变压器的原、副线圈匝数比等于10:1.这台变压器工作时,原线圈上的频率和副线圈上的频率之比等于( )
| A. | 10:1 | B. | 1:10 | C. | 1:1 | D. | 100:1 |
 如图所示,顶角为直角、质量为M的斜面体ABC放在粗糙的水平面上,∠A=30°,现沿垂直于BC方向对斜面体施加力F,斜面体仍保持静止状态.已知重力加速度为g,求斜面体受到的支持力N和摩擦力f.
如图所示,顶角为直角、质量为M的斜面体ABC放在粗糙的水平面上,∠A=30°,现沿垂直于BC方向对斜面体施加力F,斜面体仍保持静止状态.已知重力加速度为g,求斜面体受到的支持力N和摩擦力f.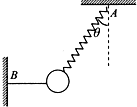 如图所示,轻质弹簧一端固定于A点,另一端悬挂一质量m=0.4kg的小球,并通过水平轻绳固定于B点,弹簧的轴线与竖直方向的夹角θ=37°,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,轻质弹簧一端固定于A点,另一端悬挂一质量m=0.4kg的小球,并通过水平轻绳固定于B点,弹簧的轴线与竖直方向的夹角θ=37°,g取10m/s2,sin37°=0.6,cos37°=0.8,求: 如图所示,有四块相同的滑块叠放起来置于水平桌面上,通过细绳和定滑轮相互联接起来.如果所有的接触面间的摩擦系数均为μ,每一滑块的质量均为m,不计滑轮的摩擦.那么要拉动最上面一块滑块至少需要多大的水平拉力?如果有n块这样的滑块叠放起来,那么要拉动最上面的滑块,至少需多大的拉力?
如图所示,有四块相同的滑块叠放起来置于水平桌面上,通过细绳和定滑轮相互联接起来.如果所有的接触面间的摩擦系数均为μ,每一滑块的质量均为m,不计滑轮的摩擦.那么要拉动最上面一块滑块至少需要多大的水平拉力?如果有n块这样的滑块叠放起来,那么要拉动最上面的滑块,至少需多大的拉力?