题目内容
15．下列说法正确的是（ ）| A． | 如果物体所受到的合外力为零，则其机械能一定守恒 | |
| B． | 如果物体所受到的合外力做功为零，则其机械能一定守恒 | |
| C． | 物体沿光滑曲面自由下滑的过程中，其机械能一定守恒 | |
| D． | 物体做匀加速运动的过程中，其机械能一定不守恒 |
分析 本题关键是两个物体构成的系统中只有动能和重力势能相互转化，机械能总量保持不变．
解答 解：A、如果物体所受到的合外力为零，则机械能不一定守恒，例如：匀速下落的降落伞的合力为零，合力做功为零，但机械能减小，AB错误；
C、物体沿光滑曲面自由下滑过程中，只有重力做功，机械能一定守恒，C正确；
D、做匀加速运动的物体，其机械能不一定守恒，比如匀加速上升，D错误；
故选：C
点评 掌握住机械能守恒的条件，也就是只有重力或者是弹力做功，动能定理是经常应用的知识点．
练习册系列答案
相关题目
5．
如图所示，实线与虚线分别表示振幅、频率均相同的两列水波的波峰和波谷，此刻，M是两列波的波峰与波峰的相遇点，下列说法中正确的是（ ）
如图所示，实线与虚线分别表示振幅、频率均相同的两列水波的波峰和波谷，此刻，M是两列波的波峰与波峰的相遇点，下列说法中正确的是（ ）| A． | 质点P始终处于平衡位置 | |
| B． | O、M两质点始终处在最大位移处 | |
| C． | 从该时刻起，经过四分之一周期，质点O到达平衡位置 | |
| D． | 随着时间的推移，质点M将向O点处移动 |
6．用m表示地球的同步卫星的质量，h表示它离地面的高度，R0表示地球的半径，g0表示地球表面的重力加速度，ω0为地球自转的角速度，则该卫星所受地球的万有引力为F，则（ ）
| A． | F=$\frac{GMm}{（{R}_{0}+h）^{2}}$ | B． | F=mω02R0 | ||
| C． | F=$\frac{m{g}_{0}{R}_{0}^{2}}{（{R}_{0}+h）^{2}}$ | D． | 轨道平面不一定与赤道平面重合 |
3．某人把原来静止于地面上的质量为2.0kg的物体向上提起1.0m，并使物体获得1.0m/s的速度，取g为10m/s2，则在此过程中（ ）
| A． | 重力对物体做功20J | B． | 人对物体做功20J | ||
| C． | 物体的机械能增加1.0J | D． | 合外力对物体做功1.0J |
10．
如图所示，物体以100J的初动能从斜面的底端向上运动，斜面足够长，当它通过斜面上的M点时，其动能减少80J，机械能减少32J，如果物体能从斜面上返回底端，则（ ）
如图所示，物体以100J的初动能从斜面的底端向上运动，斜面足够长，当它通过斜面上的M点时，其动能减少80J，机械能减少32J，如果物体能从斜面上返回底端，则（ ）| A． | 物体在斜面上运动时，机械能守恒 | |
| B． | 物体沿斜面向上运动到M点的过程中，克服摩擦力做功20J | |
| C． | 物体沿斜面向上运动到最高点的过程中，克服摩擦力做功40J | |
| D． | 物体返回到A点时的动能为20J |
20．
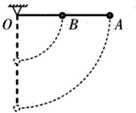如图所示，一长为L的轻质细杆可绕其一端O点的竖直平面内自由转动，在杆的中点和另一端分别固定两个质量均为m的可看作质点的A、B小球．重力加速度为g，不计空气阻力．现将杆从水平位置静止释放，从开始运动到杆刚好转动到竖直位置的过程中，下列说法正确的是（ ）
如图所示，一长为L的轻质细杆可绕其一端O点的竖直平面内自由转动，在杆的中点和另一端分别固定两个质量均为m的可看作质点的A、B小球．重力加速度为g，不计空气阻力．现将杆从水平位置静止释放，从开始运动到杆刚好转动到竖直位置的过程中，下列说法正确的是（ ）| A． | B球机械能守恒 | |
| B． | A球运动到最低点时，重力的功率为2mg$\sqrt{\frac{3gL}{5}}$ | |
| C． | B球到达最低点时的速度为$\sqrt{\frac{3gL}{5}}$ | |
| D． | 细杆对A球做功为$\frac{1}{5}$mgL |
7．
人造地球卫星绕地球的运动可看成匀速圆周运动，它们做匀速圆周运动的线速度会随着轨道半径的变化而变化，现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示，已知引力常量为G，则可求得地球质量为（ ）
人造地球卫星绕地球的运动可看成匀速圆周运动，它们做匀速圆周运动的线速度会随着轨道半径的变化而变化，现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示，已知引力常量为G，则可求得地球质量为（ ）| A． | $\frac{Ga}{b}$ | B． | $\frac{Gb}{a}$ | C． | $\frac{a}{Gb}$ | D． | $\frac{b}{Ga}$ |
4．理论和实践证明，开普勒定律不仅适用于太阳系中的天体运动，而且对一切天体（包括卫星绕行星的运动）都适用．对于开普勒第三定律的公式$\frac{{R}^{3}}{{T}^{2}}$=K，下列说法正确的是（ ）
| A． | 公式只适用于轨道是椭圆的运动 | |
| B． | 公式中的T为天体的自转周期 | |
| C． | 公式中的k值，只与中心天体有关，与绕中心天体公转的行星（或卫星）无关 | |
| D． | 若已知月球与地球之间的距离，根据开普勒第三定律公式可求出地球与太阳之间的距离 |
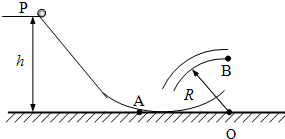如图所示，轨道由斜直轨道、凹形圆弧轨道和半径R=2.0m的圆弧管道（内径不计）组成，三部分轨道均光滑处于同一竖直平面内，且依次平滑连接，A 点为凹形圆弧轨道的最低点，B点为圆弧管道的最高点，圆弧管道的圆心O点与A点处在同一水平面上．一质量m=0.10kg、可视为质点的小球从斜直轨道上的P点无初速滑下，经过A点向B点运动，P点距A点所在水平面的高度h=2.5m，不计一切阻力，g=9.8m/s2．