题目内容
14.静水中甲、乙两只小船都处于静止状态,它们的质量均为120kg,甲船上质量为30kg的小孩以6m/s的对地速度跳上乙船,则甲、乙两船的速度大小分别为v甲=1.5m/s,v乙=1.2m/s.分析 小孩跳离甲船的过程中,甲船与小孩组成的系统在水平方向动量守恒定律,由此求得小孩跳离后甲船的速度.小孩跳到乙船上时,乙船与小孩组成的系统在水平方向动量守恒定律,由此求得小孩跳上乙船后乙船的速度.
解答 解:小孩跳离甲船的过程中,取小孩的速度方向为正方向,由动量守恒定律得 mv-m甲v甲=0
可得小孩跳离后甲船的速度为 v甲=$\frac{m}{{m}_{甲}}$v=$\frac{30}{120}$×6m/s=1.5m/s.
小孩跳上乙船的过程中,由动量守恒定律得 mv=(m乙+m)v乙,
得小孩跳上乙船后乙船的速度为 v乙=$\frac{mv}{{m}_{乙}+m}$=$\frac{30×6}{120+30}$m/s=1.2m/s.
故答案为:1.5,1.2.
点评 本题要分析清楚运动过程,分过程应用动量守恒定律即可正确解题.要注意选取正方向.

练习册系列答案
相关题目
5.在绕地球做匀速圆周运动的太空实验室内,下列仪器中可正常使用的有( )
| A. | 摆钟 | B. | 天平 | C. | 弹簧测力计 | D. | 水银温度计 |
2. 如图所示,将一根绝缘金属导线弯曲成一个完整的正弦曲线形状,它通过两个小金属环与长直金属杆M导通,图中a、b间距离为2L,导线组成的正弦图形顶部或底部到杆的距离都是d.杆的电阻不计,导线电阻为R,右边虚线范围内存在磁感应强度大小为B,方向垂直于弯曲导线所在平面的匀强磁场,磁场区域的宽度为L,现在外力作用下导线沿杆正以恒定的速度v向右运动,t=0时刻a环刚从O点进入磁场区域,则下列说法正确的是( )
如图所示,将一根绝缘金属导线弯曲成一个完整的正弦曲线形状,它通过两个小金属环与长直金属杆M导通,图中a、b间距离为2L,导线组成的正弦图形顶部或底部到杆的距离都是d.杆的电阻不计,导线电阻为R,右边虚线范围内存在磁感应强度大小为B,方向垂直于弯曲导线所在平面的匀强磁场,磁场区域的宽度为L,现在外力作用下导线沿杆正以恒定的速度v向右运动,t=0时刻a环刚从O点进入磁场区域,则下列说法正确的是( )
 如图所示,将一根绝缘金属导线弯曲成一个完整的正弦曲线形状,它通过两个小金属环与长直金属杆M导通,图中a、b间距离为2L,导线组成的正弦图形顶部或底部到杆的距离都是d.杆的电阻不计,导线电阻为R,右边虚线范围内存在磁感应强度大小为B,方向垂直于弯曲导线所在平面的匀强磁场,磁场区域的宽度为L,现在外力作用下导线沿杆正以恒定的速度v向右运动,t=0时刻a环刚从O点进入磁场区域,则下列说法正确的是( )
如图所示,将一根绝缘金属导线弯曲成一个完整的正弦曲线形状,它通过两个小金属环与长直金属杆M导通,图中a、b间距离为2L,导线组成的正弦图形顶部或底部到杆的距离都是d.杆的电阻不计,导线电阻为R,右边虚线范围内存在磁感应强度大小为B,方向垂直于弯曲导线所在平面的匀强磁场,磁场区域的宽度为L,现在外力作用下导线沿杆正以恒定的速度v向右运动,t=0时刻a环刚从O点进入磁场区域,则下列说法正确的是( )| A. | t=$\frac{L}{2v}$时刻,回路中的感应电动势为Bdv | |
| B. | t=$\frac{3L}{4v}$时刻,回路中的感应电动势为2Bdv | |
| C. | t=$\frac{L}{4v}$时刻,回路中的感应电流第一次开始改变方向 | |
| D. | 导线从进入磁场到全部出磁场,外力做功为$\frac{3{R}^{2}{d}^{2}L}{R}$ |
9. 如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
 如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )| A. | 当r<r0时,Ep随r的增大而增大 | B. | 当r>r0时,Ep随r的增大而增大 | ||
| C. | 当r<r0时,Ep不随r的变化而变化 | D. | 当r=r0时,Ep=0 |
19.下列说法正确的是( )
| A. | 物体放出热量,其内能一定减小 | |
| B. | 物体对外做功,其内能一定减小 | |
| C. | 物体放出热量,同时对外做功,其内能一定减小 | |
| D. | 物体吸收热量,同时对外做功,其内能一定减小 |
17.质量为2kg的物体做自由落体运动,经过2s落地.取g=10m/s2.关于重力做功的功率,下列说法正确的是( )
| A. | 下落过程中重力的平均功率是200W | |
| B. | 下落过程中重力的平均功率是400W | |
| C. | 落地前的瞬间重力的瞬时功率是零 | |
| D. | 落地前的瞬间重力的瞬时功率是200W |
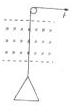 如图所示,有一等边三角形金属线框,在拉力F的作用下,以恒定速度通过匀强磁场区域(不计空气阻力).在线框从开始进入到完全进入磁场区域的这段时间内,线框平面始终保持垂直于磁感线,下边始终保持水平,线框中的发热功率P,磁感电流I,通过横截面的电荷量q以及外力F的变化可能正确的是( )
如图所示,有一等边三角形金属线框,在拉力F的作用下,以恒定速度通过匀强磁场区域(不计空气阻力).在线框从开始进入到完全进入磁场区域的这段时间内,线框平面始终保持垂直于磁感线,下边始终保持水平,线框中的发热功率P,磁感电流I,通过横截面的电荷量q以及外力F的变化可能正确的是( )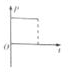
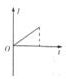
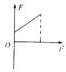
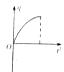
 如图所示,一长为l的轻绳,一端穿在过O点的水平转轴上,另一端栓有一质量未知的小球,整个装置绕O点在竖直面内转动.小球通过最高点时,绳对小球的拉力F与其速度的水平v2的关系如图乙所示,已知图象的横截距的大小为b.
如图所示,一长为l的轻绳,一端穿在过O点的水平转轴上,另一端栓有一质量未知的小球,整个装置绕O点在竖直面内转动.小球通过最高点时,绳对小球的拉力F与其速度的水平v2的关系如图乙所示,已知图象的横截距的大小为b.