题目内容
15. 如图所示,以v0=10m/s的速度水平抛出的小球,飞行一段时间垂直地撞在倾角θ=30°的斜面上,按g=10m/s2考虑,则物体飞行时间是$\sqrt{3}s$物体撞击斜面时的速度大小20m/s.
如图所示,以v0=10m/s的速度水平抛出的小球,飞行一段时间垂直地撞在倾角θ=30°的斜面上,按g=10m/s2考虑,则物体飞行时间是$\sqrt{3}s$物体撞击斜面时的速度大小20m/s.
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,将速度进行分解,根据平行四边形定则求出撞在斜面上竖直方向上的分速度,从而根据速度时间公式求出运动的时间,根据平行四边形定则求出物体撞击斜面时的速度.
解答  解:根据tan30°=$\frac{{v}_{0}}{{v}_{y}}$得,竖直分速度${v}_{y}=\frac{10}{\frac{\sqrt{3}}{3}}m/s=10\sqrt{3}m/s$,
解:根据tan30°=$\frac{{v}_{0}}{{v}_{y}}$得,竖直分速度${v}_{y}=\frac{10}{\frac{\sqrt{3}}{3}}m/s=10\sqrt{3}m/s$,
则物体飞行的时间t=$\frac{{v}_{y}}{g}=\frac{10\sqrt{3}}{10}s=\sqrt{3}s$.
根据平行四边形定则知,物体撞击斜面时的速度v=$\frac{{v}_{0}}{sin30°}=\frac{10}{\frac{1}{2}}m/s=20m/s$.
故答案为:$\sqrt{3}s$,20m/s.
点评 本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解,要抓住题目隐含的条件,运用运动的分解法解答.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
5.在物理学的发展中,物理学家们进行了不懈的努力,以下关于物理学史和物理学研究方法的叙述不正确的是( )
| A. | 在推导匀变速直线运动位移公式时,把整个运动过程等分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里运用了微元法 | |
| B. | 牛顿提出物体都具有保持原来运动状态的属性,即惯性 | |
| C. | 在验证力的平行四边形定则中采用了控制变量法 | |
| D. | 伽利略根据理想实验推出,如果没有摩擦,在水平面上的物体,一旦具有某一个速度,将保持这个速度继续运动下去 |
3.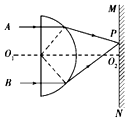 如图所示,O1O2是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于O1O2轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于O1O2放置的光屏,沿O1O2方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )
如图所示,O1O2是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于O1O2轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于O1O2放置的光屏,沿O1O2方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )
 如图所示,O1O2是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于O1O2轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于O1O2放置的光屏,沿O1O2方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )
如图所示,O1O2是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于O1O2轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于O1O2放置的光屏,沿O1O2方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )| A. | 该玻璃体对A光的折射率比对B光的折射率小 | |
| B. | A光从空气进入该玻璃体后,其频率变高 | |
| C. | 在该玻璃体中,A光比B光的传播速度大 | |
| D. | 在真空中,A光的波长比B光的波长长 |
10.对于一个已经带电的物体,下列说法中正确的是( )
| A. | 物体上一定有多余的电子 | B. | 物体上一定缺少电子 | ||
| C. | 物体的带电量一定是e整数倍 | D. | 物体的带电量可以是任意的一个值 |
7.下列物理量中属于矢量的是( )
| A. | 功率 | B. | 功 | C. | 向心加速度 | D. | 重力势能 |
4.障碍物宽度为10cm,下列各种波长中的波能出现最明显的衍射现象的波长是( )
| A. | 5cm | B. | 20cm | C. | 50cm | D. | 80cm |
 如图所示是一个半径为R的$\frac{1}{4}$圆柱体棱镜的截面图,棱镜的直角边紧贴在x、y轴上.一束细光线平行于x轴从P点射入圆柱形棱镜中,投射到N点,经棱镜折射后从x轴上的Q点穿过,P点到圆心O的距离是$\frac{R}{2}$,O点到圆心O的距离是$\sqrt{3R}$,求:
如图所示是一个半径为R的$\frac{1}{4}$圆柱体棱镜的截面图,棱镜的直角边紧贴在x、y轴上.一束细光线平行于x轴从P点射入圆柱形棱镜中,投射到N点,经棱镜折射后从x轴上的Q点穿过,P点到圆心O的距离是$\frac{R}{2}$,O点到圆心O的距离是$\sqrt{3R}$,求:
 如图,一内壁光滑、截面恒定、竖直放置的绝热气缸下端密封,上端封闭但留有一出气孔.气缸内部有一绝热活塞,将气缸内的气体(可视为理想气体)分割成上下两部分,气缸底部有一用来加热气体的电阻丝,外界大气压强为 p.当气体温度为 T 时,活塞下方气体的体积为 V,活塞上方气体的体积为 8V;现将气缸水平放置,这一过程温度不变,活塞下方这部分气体的体积变为 2V,此时将出气孔密封.然后重新将气缸竖直放置,并对下部分气体加热.求:
如图,一内壁光滑、截面恒定、竖直放置的绝热气缸下端密封,上端封闭但留有一出气孔.气缸内部有一绝热活塞,将气缸内的气体(可视为理想气体)分割成上下两部分,气缸底部有一用来加热气体的电阻丝,外界大气压强为 p.当气体温度为 T 时,活塞下方气体的体积为 V,活塞上方气体的体积为 8V;现将气缸水平放置,这一过程温度不变,活塞下方这部分气体的体积变为 2V,此时将出气孔密封.然后重新将气缸竖直放置,并对下部分气体加热.求: