题目内容
13. 如图所示,一质量为M的平板车B放在光滑水平面上,在其左端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现同时给A和B大小相等、方向相反的初速度v0,使A开始向右运动,B开始向左运动,最后A不会滑离B.求:
如图所示,一质量为M的平板车B放在光滑水平面上,在其左端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现同时给A和B大小相等、方向相反的初速度v0,使A开始向右运动,B开始向左运动,最后A不会滑离B.求:(1)A在B上相对滑动的距离;
(2)A在B上相对滑动的时间.
分析 (1)A、B组成的系统动量守恒,由动量守恒定律可以求出它们的最终速度.A在B上先减速后反向加速,求出二者间的相对位移.
(2)对A(或B)应用动量定理可以求出A在B上滑行的时间.
解答 解:(1)A不会滑离B板,说明A、B相对静止时,A、B具有相同的速度,
A、B组成的系统动量守恒,以A、B组成的系统为研究对象,以B的初速度方向为正方向,
由动量守恒定律得:Mv0-mv0=(M+m)v,解得:v=$\frac{M-m}{M+m}$v0,因M>m,v>0,方向向左;
对整体应用动能定理得:-$μmgl=\frac{1}{2}(M+m){v}^{2}-\frac{1}{2}(M+m){v}_{0}^{2}$
求得最短长车 $l=\frac{3{v}_{0}^{2}}{2μg}$
(2)设木块在木板上相对滑动的时间为t,以向左为正方向,
对木块由动量定理得:μmgt=mv-m(-v0),解得:t=$\frac{v+{v}_{0}}{μg}$=$\frac{2M{v}_{0}}{μ(m+M)g}$;
答:(1)A在B上相对滑动的距离为$\frac{3{v}_{0}^{2}}{2μg}$;
(2)A在B上相对滑动的时间为$\frac{2M{v}_{0}}{μ(m+M)g}$.
点评 本题考查了求速度与滑动时间,应用动量守恒定律与动量定理即可正确解题,解题时注意正方向的选择.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
3. 将小球以10m/s的初速从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能EP与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能EP与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
 将小球以10m/s的初速从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能EP与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能EP与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )| A. | 小球的质量为0.2kg | |
| B. | 小球受到的阻力(不包括重力)大小为0.20N | |
| C. | 小球动能与重力势能相等时的高度为$\frac{20}{13}$m | |
| D. | 小球上升到2m时,动能与重力势能之差为0.5J |
4. 近来,我国大部分地区都出现了雾霾天气,给人们的正常生活造成了极大的影响,在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.如图a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
近来,我国大部分地区都出现了雾霾天气,给人们的正常生活造成了极大的影响,在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.如图a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
 近来,我国大部分地区都出现了雾霾天气,给人们的正常生活造成了极大的影响,在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.如图a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
近来,我国大部分地区都出现了雾霾天气,给人们的正常生活造成了极大的影响,在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.如图a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )| A. | 因刹车失灵前小汽车已减速,不会追尾 | |
| B. | 在t=3s时追尾 | |
| C. | 在t=5s时追尾 | |
| D. | 由于初始距离太近,即使刹车不失灵也会追尾 |
8. 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )
 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )| A. | 用交流电流表测得通过R1的电流为4A | |
| B. | 用交流电流表测得通过R2的电流为$\sqrt{2}$A | |
| C. | 变压器的输入功率为600W | |
| D. | 副线圈中电流的有效值为6A |
5. 如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )
如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )
 如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )
如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )| A. | 线圈中感应电动势的表达式为e=125$\sqrt{2}$cos(100t)V | |
| B. | P上移电流表读数不变 | |
| C. | 当原副线圈匝数比为2:1时,电流表示数为$\sqrt{2}$A | |
| D. | 当原副线圈匝数比为2:1时,电阻R上消耗的功率为120W |
2.如图所示,将一长方形木块锯开为A、B两部分后,静止放置在水平地面上.则( )


| A. | B受到四个力作用 | |
| B. | B受到五个力作用 | |
| C. | A对B的作用力方向竖直向下 | |
| D. | A对B的作用力方向垂直于它们的接触面向下 |
3. 四个相同的电流表分别改装成两个安培表和两个电压表,安培表A1的量程大于A2的量程,电压表V1的量程大于V2的量程,把它们按图接入电路中( )
四个相同的电流表分别改装成两个安培表和两个电压表,安培表A1的量程大于A2的量程,电压表V1的量程大于V2的量程,把它们按图接入电路中( )
 四个相同的电流表分别改装成两个安培表和两个电压表,安培表A1的量程大于A2的量程,电压表V1的量程大于V2的量程,把它们按图接入电路中( )
四个相同的电流表分别改装成两个安培表和两个电压表,安培表A1的量程大于A2的量程,电压表V1的量程大于V2的量程,把它们按图接入电路中( )| A. | A1的读数比A2的读数大 | |
| B. | A1指针偏转角度比A2指针偏转角度大 | |
| C. | V1读数比V2读数大 | |
| D. | V1指针偏转角度比V2指针偏转角度大 |
 如图所示CDPD′M是螺旋光滑绝缘轨道,半径为R1=2m的一段圆弧CD与半径为R2=1m的圆O相切于最低点D,D′M是与圆轨道相切于D′点的水平轨道,在M端固定一个水平放置的轻弹簧,其中PC与竖直方向成 θ=53°.在半径为R2的圆内区域有垂直纸面向外的匀强磁场,在圆O的竖直直径POD的右方区域存在一个水平向右,大小为E=10N/C的匀强电场.现有一质量为m=0.04kg、电量为q=0.2C的带电小球,从离水平轨道D′M 高为h=1.6m的A点以某一水平初速度抛出,刚好沿CD弧的切线方向无碰撞地进入CD轨道,经D点进入竖直圆轨道之后,刚好能通过圆轨道的最高点P,之后从最低点D′点进入水平轨道D′M并压缩弹簧,在距离D′点为L=2m 的地方速度减为零.不计带电小球电量对电场的影响,g=10m/s2,(sin53°=0.8,cos53°=0.6)求:
如图所示CDPD′M是螺旋光滑绝缘轨道,半径为R1=2m的一段圆弧CD与半径为R2=1m的圆O相切于最低点D,D′M是与圆轨道相切于D′点的水平轨道,在M端固定一个水平放置的轻弹簧,其中PC与竖直方向成 θ=53°.在半径为R2的圆内区域有垂直纸面向外的匀强磁场,在圆O的竖直直径POD的右方区域存在一个水平向右,大小为E=10N/C的匀强电场.现有一质量为m=0.04kg、电量为q=0.2C的带电小球,从离水平轨道D′M 高为h=1.6m的A点以某一水平初速度抛出,刚好沿CD弧的切线方向无碰撞地进入CD轨道,经D点进入竖直圆轨道之后,刚好能通过圆轨道的最高点P,之后从最低点D′点进入水平轨道D′M并压缩弹簧,在距离D′点为L=2m 的地方速度减为零.不计带电小球电量对电场的影响,g=10m/s2,(sin53°=0.8,cos53°=0.6)求: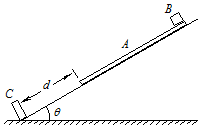 如图所示,光滑斜面倾角为θ,底端固定一垂直于斜面的挡板C,在斜面上放置长木板A,A的下端与C的距离为d,A的上端放置小物块B,A、B的质量均为m,A、B间的动摩擦因数μ=$\frac{3}{2}$tanθ,现同时由静止释放A,B、A与C发生碰撞的时间极短,碰撞前后瞬间速度大小相等,运动过程中小物块始终没有从木板上滑落,已知重力加速度为g,求
如图所示,光滑斜面倾角为θ,底端固定一垂直于斜面的挡板C,在斜面上放置长木板A,A的下端与C的距离为d,A的上端放置小物块B,A、B的质量均为m,A、B间的动摩擦因数μ=$\frac{3}{2}$tanθ,现同时由静止释放A,B、A与C发生碰撞的时间极短,碰撞前后瞬间速度大小相等,运动过程中小物块始终没有从木板上滑落,已知重力加速度为g,求