题目内容
10. 如图所示,在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=1.5m的薄平板AB.平板的上表面光滑,其下端B与斜面底端C的距离为10.5m,在平板的上端A处放一质量m=0.5kg的滑块P(可视为质点),开始时使平板和滑块都静止,之后将它们无初速释放.平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.25,已知sin37°=0.6,cos37°=0.8,g=10m/s2,求:
如图所示,在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=1.5m的薄平板AB.平板的上表面光滑,其下端B与斜面底端C的距离为10.5m,在平板的上端A处放一质量m=0.5kg的滑块P(可视为质点),开始时使平板和滑块都静止,之后将它们无初速释放.平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.25,已知sin37°=0.6,cos37°=0.8,g=10m/s2,求:(1)滑块P离开平板时的速度;
(2)平板下端B到达斜面底端C的时间与P到达C点的时间差.
分析 分别研究滑块与平板的运动情况:开始时,由于Mgsin37°<μ(M+m)gcos37°,滑块在平板上滑动时,平板静止不动.根据牛顿第二定律求出滑块的加速度,由位移-速度关系式求出滑块到达B点时的速度.滑块离开平板后,根据牛顿第二定律求出滑块沿斜面下滑的加速度,由位移公式求解滑块由B至C所用时间.滑块滑离后平板才开始运动,根据牛顿第二定律求出平板沿斜面下滑的加速度,由位移公式求解滑块由B至C所用时间.再求解时间差.
解答  解:(1)当P离开薄板前,受力如图,由牛顿第二定律得:mgsinθ=mam1
解:(1)当P离开薄板前,受力如图,由牛顿第二定律得:mgsinθ=mam1
当P离开薄板前,薄板受力如图,由牛顿第二定律、平衡条件、摩擦力公式得:Mgsinθ-fM1=MaM1
NM1=Mgcosθ+Nm′
fM1=μNM1
Nm′=Nm=mgcosθ
由匀变速运动规律得:${s_m}=\frac{1}{2}{a_{m1}}t_1^2$
${s_M}=\frac{1}{2}{a_{M1}}t_1^2$
vm1=am1t1
由题意得:sm-sM=L
联立以上各式并代入数据解得:vm1=6m/s
(2)当P离开薄板后,受力如图,由牛顿第二定律、摩擦力公式得:mgsinθ-fm=mam2fm=μNm
当P离开薄板后,薄板受力如图,由牛顿第二定律、平衡条件、摩擦力公式得:
Mgsinθ-fM2=MaM2
NM2=MgcosθfM2=μNM2
由匀变速运动规律得:${s_{BC}}-{s_M}={v_{m1}}{t_2}+\frac{1}{2}{a_{m2}}t_2^2$
${s_{BC}}-{s_M}={v_{M1}}{t_3}+\frac{1}{2}{a_{M2}}t_3^2$
vM1=aM1t1
联立以上各式并代入数据解得:△t=t3-t2=0.5s
答:(1)滑块P离开平板时的速度为6m/s;
(2)平板下端B到达斜面底端C的时间与P到达C点的时间差为0.5s.
点评 本题关键在于分析两物体的受力情况,再确定物体的运动情况.也可以运用动能定理与运动学公式结合求解.

 1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图,则下列正确的是( )
1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图,则下列正确的是( )| A. | 该束带电粒子带正电 | |
| B. | 该束带电粒子带负电 | |
| C. | 速度选择器的P1极板带正电 | |
| D. | 在B2磁场中运动半径越大的粒子,比荷$\frac{q}{m}$越小 |
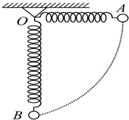 如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下.不计空气阻力,在重物由A点摆向最低点B的过程中( )
如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下.不计空气阻力,在重物由A点摆向最低点B的过程中( )| A. | 重物的重力势能增加 | B. | 弹簧的弹性势能不变 | ||
| C. | 重物的机械能减少 | D. | 重物和弹簧组成的系统机械能减少 |
 如图所示,重物B被绕过小滑轮P的细线所悬挂,重物A放在粗糙的水平桌面上;小滑轮P被一根斜短线系于天花板上的Q点;O是三根线的结点,AO水平拉着A物体,C沿竖直方向拉着弹簧,CO与PO夹角为120°;弹簧、细线、滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.其中A重100N,B重40N,A与桌面间的动摩擦因数为0.5,则下列说法正确的是( )
如图所示,重物B被绕过小滑轮P的细线所悬挂,重物A放在粗糙的水平桌面上;小滑轮P被一根斜短线系于天花板上的Q点;O是三根线的结点,AO水平拉着A物体,C沿竖直方向拉着弹簧,CO与PO夹角为120°;弹簧、细线、滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.其中A重100N,B重40N,A与桌面间的动摩擦因数为0.5,则下列说法正确的是( )| A. | 弹簧的弹力大小为20N | B. | 桌面对A的摩擦力大小为50N | ||
| C. | 线CO与PO拉力的合力大小为20$\sqrt{3}$N | D. | 线QP与竖直方向的夹角为60° |
 质量为m的三角形木楔A置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数为μ,一水平力F作用在木楔A的竖直平面上,在力F的推动下,木楔A沿斜面以恒定的加速度a向上滑动,则F的大小为( )
质量为m的三角形木楔A置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数为μ,一水平力F作用在木楔A的竖直平面上,在力F的推动下,木楔A沿斜面以恒定的加速度a向上滑动,则F的大小为( )| A. | $\frac{m(a-gsinθ)}{cosθ+μsinθ}$ | B. | $\frac{m[a+g(sinθ+μcosθ)]}{cosθ-μsinθ}$ | ||
| C. | $\frac{m(a+μgcosθ)}{cosθ}$ | D. | $\frac{{m[{a+g(sinθ+μcosθ)}]}}{cosθ}$ |
| A. | 弹簧秤、细绳、橡皮条都应与木板平行 | |
| B. | 两细绳之间的夹角越大越好 | |
| C. | 用两弹簧秤同时拉细绳时两弹簧秤示数之差应尽可能大 | |
| D. | 拉橡皮条的细绳要长些,标记同一细绳方向的两点要远些 |




 某同学利用电压表和电阻箱测定一种特殊电池的电动势,该同学利用如图所示的电路进行实验,图中R0为已知阻值的定值电阻.
某同学利用电压表和电阻箱测定一种特殊电池的电动势,该同学利用如图所示的电路进行实验,图中R0为已知阻值的定值电阻.