��Ŀ����
14�� ��ͼ��ʾ��С��a��b�ó��Ⱦ�ΪL��ϸ��������ͬһ�̶���O������a��ֹ�´�������b��������ʹϸ��ˮƽ��ֱ���ɾ�ֹ�ͷ���b����������ճ��һ������ڶ����˺�ϸ������ֱ����֮������ƫ�Ǧ�=60�㣮���Կ����������������ٶȴ�СΪg��
��ͼ��ʾ��С��a��b�ó��Ⱦ�ΪL��ϸ��������ͬһ�̶���O������a��ֹ�´�������b��������ʹϸ��ˮƽ��ֱ���ɾ�ֹ�ͷ���b����������ճ��һ������ڶ����˺�ϸ������ֱ����֮������ƫ�Ǧ�=60�㣮���Կ����������������ٶȴ�СΪg����1����������ײǰ˲�䣬С��b���ٶȴ�С��
��2�������������֮�ȣ�
��3������С���˶�����͵����ڵ�ˮƽ��Ϊ�������棬��a��b������ɵ�ϵͳ����ײǰ��Ļ�е��֮�ȣ�
���� ��1��b���°ڹ����У�ֻ�������������ɻ�е���غ㶨�������ǰb����ٶȣ�
��2��������ײ�����ж����غ㣬�ɶ����غ㶨���з��̣�������������ڶ������У�����Ļ�е���غ㣬�ɻ�е���غ㶨����ʽ��������������������֮�ȣ�
��3������������ײǰ���ɻ�е���غ㶨�ɵó����ǵĻ�е�ܣ�����ϵͳ����ײǰ��Ļ�е��֮�ȣ�
��� �⣺��1������a������Ϊm1����b������Ϊm2������b�ڵ���͵㣬��δ����a����ʱ���ٶȴ�СΪv���ɶ��ܶ�����
m2gL=$\frac{1}{2}{m}_{2}{v}^{2}$
��� v=$\sqrt{2gL}$
��2��������˲������Ĺ�ͬ�ٶ�Ϊv�䣮���������ײ������ڵ����λ�õĹ����У��ɶ��ܶ�����
-��m1+m2��gL��1-cos60�㣩=0-$\frac{1}{2}��{m}_{1}+{m}_{2}��v{��}^{2}$
��� v��=$\sqrt{gL}$
������ײ���̣���ˮƽ����Ϊ�������ɶ����غ㶨�ɵ�
m2v=��m1+m2��v��
��� $\frac{{m}_{1}}{{m}_{2}}$=$\sqrt{2}$-1
��3��a��b������ɵ�ϵͳ����ײǰ�Ļ�е��Ϊ E1=m2gL
a��b������ɵ�ϵͳ����ײ��Ļ�е��Ϊ E2=m2gL��1-cos60�㣩
��� $\frac{{m}_{1}}{{m}_{2}}$=$\sqrt{2}$-1
��� $\frac{{E}_{1}}{{E}_{2}}$=$\sqrt{2}$
��
��1��������ײǰ˲�䣬С��b���ٶȴ�С��$\sqrt{2gL}$��
��2�����������֮��Ϊ$\sqrt{2}$-1��
��3��a��b������ɵ�ϵͳ����ײǰ��Ļ�е��֮��Ϊ$\sqrt{2}$��1��
���� �������Ĺؼ���Ҫ��ȷС�����°ڻ��ϰڹ����л�е���غ㣬��ײ�����ж����غ㣬�ɶ��ܶ��������е���غ㶨�ɣ��������غ㶨�ɼ�����ȷ���⣮

| A�� | �����ߵĹᴩ����Ȧ�����ǿ | |
| B�� | ������Ϊԭ�ӵĺ�����ӵ�����γɵĵ����� | |
| C�� | �ü��¡���ѹ��ı��仯ѧ״̬�ķ��������ܸı�ԭ�Ӻ�˥��İ�˥�� | |
| D�� | ԭ�Ӻ˾���˥�������ºˣ����º˵������ܵ���ԭ�˵����� |
| A�� | С���ɺӵ����ʱ��Ϊ20s | |
| B�� | ҪʹС���ɺӵ�λ����̣�������Ӱ�����Ӧ��ֱ | |
| C�� | ���ɺӵ���Сλ��Ϊ100m | |
| D�� | ���ɺӵ���Сλ��Ϊ125m |
 һ����Ϊ0.5kg��С���ع⻬ˮƽ���СΪ5m/s���ٶ�ˮƽ�����˶�����ǽ����ײ���Դ�СΪ3m/s���ٶȷ��أ���֪С���ǽ�����õ�ʱ��Ϊ0.05s����ù�����С���ܵ�ǽ�ڵ�ƽ����������������
һ����Ϊ0.5kg��С���ع⻬ˮƽ���СΪ5m/s���ٶ�ˮƽ�����˶�����ǽ����ײ���Դ�СΪ3m/s���ٶȷ��أ���֪С���ǽ�����õ�ʱ��Ϊ0.05s����ù�����С���ܵ�ǽ�ڵ�ƽ����������������| A�� | ��СΪ80N������ˮƽ���� | B�� | ��СΪ80N������ˮƽ���� | ||
| C�� | ��СΪ20N������ˮƽ���� | D�� | ��СΪ20N������ˮƽ���� |
| A�� | ��������æ����Ӻ����ˣ����������� | |
| B�� | ���ʿ�����˹���˵���������˹��ЧӦ���� | |
| C�� | ¬ɪ��ͨ��������ɢ��ʵ�飬֤ʵ����ԭ�Ӻ��ڴ������� | |
| D�� | �����ն�ͨ������Ȼ����������о���������ԭ���д��ڵ�ԭ�Ӻ� |
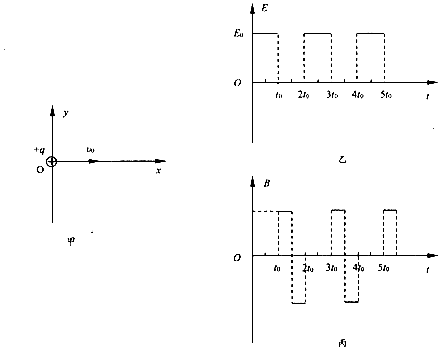 ����ͼ����ʾ��xOyƽ���ڣ�y���Ҳ�ռ��зֲ����ȡ���С��ʱ�������Ա仯�ĵ糡�ʹų�����仯���ɷֱ���ͼ�ҡ�����ʾ���糡ǿ�ȴ�СΪE0��������y�Ḻ����ֱxOyƽ������Ϊ�ų�����������t=0ʱ�̣�����Ϊm�������Ϊ+q�����ӣ��Գ��ٶȴ�СΪ��0������ԭ��O��x���������������֪�����ڴų�����Բ���˶�������Ϊt0���������ӵ��������������ڣ�
����ͼ����ʾ��xOyƽ���ڣ�y���Ҳ�ռ��зֲ����ȡ���С��ʱ�������Ա仯�ĵ糡�ʹų�����仯���ɷֱ���ͼ�ҡ�����ʾ���糡ǿ�ȴ�СΪE0��������y�Ḻ����ֱxOyƽ������Ϊ�ų�����������t=0ʱ�̣�����Ϊm�������Ϊ+q�����ӣ��Գ��ٶȴ�СΪ��0������ԭ��O��x���������������֪�����ڴų�����Բ���˶�������Ϊt0���������ӵ��������������ڣ�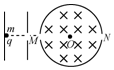 һԲͲ�ĺ������ͼ��ʾ��Բ��ΪO���뾶ΪR����Ͳ��������С��M��N��M��O��N��ͬһˮƽ���ϣ�ԲͲ���������д�ֱ��ԲͲ�������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����ԲͲ�����һ�����ٵ糡��һ������Ϊm�������Ϊq�Ĵ��������ӣ��ɾ�ֹ���糡���ٺ��M����MO��������ԲͲ����֪������ԲͲ��ײʱ��������ֲ��䣬��ײ���ٶȴ�С���䣬��������ײǰ�෴����������������
һԲͲ�ĺ������ͼ��ʾ��Բ��ΪO���뾶ΪR����Ͳ��������С��M��N��M��O��N��ͬһˮƽ���ϣ�ԲͲ���������д�ֱ��ԲͲ�������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����ԲͲ�����һ�����ٵ糡��һ������Ϊm�������Ϊq�Ĵ��������ӣ��ɾ�ֹ���糡���ٺ��M����MO��������ԲͲ����֪������ԲͲ��ײʱ��������ֲ��䣬��ײ���ٶȴ�С���䣬��������ײǰ�෴���������������� ��ͼ��ʾ��MN��PQΪ��б���õ��㹻����ƽ�й⻬���죬������ΪL�����Ϊ�ȣ������ӵĵ�����ֵΪR��MN��PQ��λ���ȵ���Ϊr0������װ�ô��ڴŸ�Ӧǿ��ΪB������ֱ����ƽ�����ϵ���ǿ�ų��У�������ab��ֱ�ڵ�����ã�t=0ʱ���������ڵ���ײ�������������Ϊm�����ƽ��������裮�ڽ������м�ϵһϸ�ߣ�ϸ��ͨ���⻬��������ֱ����ʩ��������F��ʹ��Ӿ�ֹ��ʼ�Լ��ٶ�a�ص����������ȼ���ֱ���˶����������ٶ�Ϊg���������뵼��ʼ�սӴ����ã�
��ͼ��ʾ��MN��PQΪ��б���õ��㹻����ƽ�й⻬���죬������ΪL�����Ϊ�ȣ������ӵĵ�����ֵΪR��MN��PQ��λ���ȵ���Ϊr0������װ�ô��ڴŸ�Ӧǿ��ΪB������ֱ����ƽ�����ϵ���ǿ�ų��У�������ab��ֱ�ڵ�����ã�t=0ʱ���������ڵ���ײ�������������Ϊm�����ƽ��������裮�ڽ������м�ϵһϸ�ߣ�ϸ��ͨ���⻬��������ֱ����ʩ��������F��ʹ��Ӿ�ֹ��ʼ�Լ��ٶ�a�ص����������ȼ���ֱ���˶����������ٶ�Ϊg���������뵼��ʼ�սӴ����ã�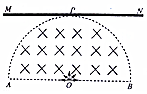 ��ͼ��ʾΪһ����ֱֽ������İ�Բ����ǿ�ų�����OΪ��Բ�ģ�ABΪ��ֱ�����㹻�����ռ���MNƽ����AB�����Բ������������P�㣮O�����һ����Դ������OA��OB֮��180�㷶Χ����ų���������������Ϊv0�Ĵ��������ӣ���֪AB=2L�����ӵ�������Ϊm�����������Ϊq���������ӵ������Լ�����ã�
��ͼ��ʾΪһ����ֱֽ������İ�Բ����ǿ�ų�����OΪ��Բ�ģ�ABΪ��ֱ�����㹻�����ռ���MNƽ����AB�����Բ������������P�㣮O�����һ����Դ������OA��OB֮��180�㷶Χ����ų���������������Ϊv0�Ĵ��������ӣ���֪AB=2L�����ӵ�������Ϊm�����������Ϊq���������ӵ������Լ�����ã�