题目内容
11. 如图所示,光滑的曲面轨道AB高h=0.8m,与粗糙的水平轨道BD平滑连接.一质量为m=2.0kg的物块自轨道顶端A点从静止开始下滑,然后沿水平轨道向右运动到C点停下.B、C间的距离x=1.6m,重力加速度g取10m/s2.求:
如图所示,光滑的曲面轨道AB高h=0.8m,与粗糙的水平轨道BD平滑连接.一质量为m=2.0kg的物块自轨道顶端A点从静止开始下滑,然后沿水平轨道向右运动到C点停下.B、C间的距离x=1.6m,重力加速度g取10m/s2.求:(1)物块滑到轨道B点时的速度大小;
(2)物块与水平轨道BC之间的动摩擦因数μ.
分析 (1)对物体由A到B过程由机械能守恒定律可知物体滑到B点时的速度大小;
(2)对物体从B到C过程,根据动能定理可求得BC之间的动摩擦因数大小.
解答 解:(1)物块从A到B,由机械能守恒定律得$mgh=\frac{1}{2}mv_B^2$
解得 ${v_B}=\sqrt{2gh}$=$\sqrt{2×10×0.8}$=4m/s
(2)物块从B到C,由动能定理得 $-fx=0-\frac{1}{2}mv_B^2$
其中 f=μmg
联立解得μ=$\frac{v_B^2}{2gx}$=$\frac{16}{2×10×1.6}$=0.5
答:(1)物块滑到轨道B点时的速度大小为4m/s
(2)物块与水平轨道BC之间的动摩擦因数μ为0.5.
点评 本题考查动能定理以及机械能守恒定律的应用,解题时要注意明确物理过程,根据受力情况正确选择物理规律求解即可.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
2.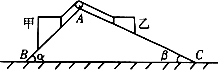 如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接后分别静止在斜面AB、AC 上,滑轮两例细绳与斜面平行.甲、乙两物块的质量分别为m1、m2,AB斜面粗糙,傾角为α,AC斜面光滑,傾角β,不计滑轮处摩擦,则以下分析正确的是( )
如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接后分别静止在斜面AB、AC 上,滑轮两例细绳与斜面平行.甲、乙两物块的质量分别为m1、m2,AB斜面粗糙,傾角为α,AC斜面光滑,傾角β,不计滑轮处摩擦,则以下分析正确的是( )
 如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接后分别静止在斜面AB、AC 上,滑轮两例细绳与斜面平行.甲、乙两物块的质量分别为m1、m2,AB斜面粗糙,傾角为α,AC斜面光滑,傾角β,不计滑轮处摩擦,则以下分析正确的是( )
如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接后分别静止在斜面AB、AC 上,滑轮两例细绳与斜面平行.甲、乙两物块的质量分别为m1、m2,AB斜面粗糙,傾角为α,AC斜面光滑,傾角β,不计滑轮处摩擦,则以下分析正确的是( )| A. | m1sinα>m2sinβ,则甲所受的摩擦力沿斜面向下 | |
| B. | m1sinα<m2sinβ,则甲所受的摩擦力沿斜面向下 | |
| C. | 若在物块乙上面再放一个小物块后,甲、乙仍静止,则甲所受的拉力一定变大 | |
| D. | 若在物块甲上面再放一个小物块后,甲、乙仍静止,则甲所受的拉力一定变大 |
19.对于某一温度下大量气体分子的无规则运动,下列说法中正确的是( )
| A. | 所有分子的速率都相同 | |
| B. | 每个分子都有一个确定的速率 | |
| C. | 多数分子速率都在某个数值附近 | |
| D. | 我们可以掌握每个分子运动的全部信息 |
 滑雪运动是把滑雪板装在靴底上在雪地上进行速度、跳跃和滑降的竞赛运动.滑雪运动中当滑雪板相对雪地速度较大时,会把雪内的空气逼出来,在滑雪板与雪地间形成一个暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦.然而当滑雪板相对雪地速度较小时,与雪地接触时间超过某一值就会陷下去,使得它们间的摩擦力增大.假设滑雪者的速度超过8m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125.一滑雪者从倾角θ=37°的坡顶A处由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平地面,最后停在C处,如图所示.不计空气阻力,已知坡长L=24.1m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
滑雪运动是把滑雪板装在靴底上在雪地上进行速度、跳跃和滑降的竞赛运动.滑雪运动中当滑雪板相对雪地速度较大时,会把雪内的空气逼出来,在滑雪板与雪地间形成一个暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦.然而当滑雪板相对雪地速度较小时,与雪地接触时间超过某一值就会陷下去,使得它们间的摩擦力增大.假设滑雪者的速度超过8m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125.一滑雪者从倾角θ=37°的坡顶A处由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平地面,最后停在C处,如图所示.不计空气阻力,已知坡长L=24.1m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求: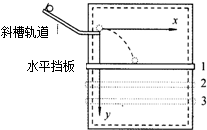 某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学做了三次实验,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )
某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学做了三次实验,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( ) 质量为m的光滑小球用绳拉住,放在倾角为30°的固定斜面上处于静止状态,绳与竖直方向成30°角,如图所示,则绳的拉力大小为$\frac{\sqrt{3}}{3}mg$,斜面对球的支持力大小为$\frac{\sqrt{3}}{3}mg$.
质量为m的光滑小球用绳拉住,放在倾角为30°的固定斜面上处于静止状态,绳与竖直方向成30°角,如图所示,则绳的拉力大小为$\frac{\sqrt{3}}{3}mg$,斜面对球的支持力大小为$\frac{\sqrt{3}}{3}mg$. 如图所示,质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉,已知OP=$\frac{L}{2}$,在A点给小球一个水平向左的初速度v0=2$\sqrt{gL}$,发现小球恰能到达跟P点在同一竖直线上的最高点B.则:
如图所示,质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉,已知OP=$\frac{L}{2}$,在A点给小球一个水平向左的初速度v0=2$\sqrt{gL}$,发现小球恰能到达跟P点在同一竖直线上的最高点B.则: