题目内容
木星是太阳系中最大的行星,它有众多卫星.观察测出:木星绕太阳作圆周运动的半径为r1、周期为T1;木星的某一卫星绕木星作圆周运动的半径为r2、周期为T2.已知万有引力常量为G,则根据题中给定条件( )A.能求出木星的质量
B.能求出木星与卫星间的万有引力
C.能求出太阳与木星间的万有引力
D.可以断定
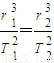
【答案】分析:木星绕太阳作圆周运动,根据万有引力提供向心力,列出等式.
某一卫星绕木星作圆周运动,根据万有引力提供向心力,列出等式.
根据题目中已知物理量判断能够求出的物理量.
运用开普勒第三定律求解问题.
解答:解:A、某一卫星绕木星作圆周运动,根据万有引力提供向心力,列出等式:
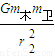 =m卫
=m卫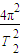 r2
r2
m木=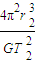
故A正确.
B、由于不知道卫星的质量,所以不能求出木星与卫星间的万有引力,故B错误.
C、太阳与木星间的万有引力提供木星做圆周运动所需要的向心力,
太阳与木星间的万有引力F=m木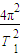 r1=
r1=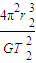 ?
?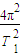 r1=
r1=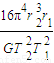
故C正确.
D、根据开普勒第三定律为: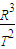 =k,其中我们要清楚k与中心体的质量有关,与环绕体无关.
=k,其中我们要清楚k与中心体的质量有关,与环绕体无关.
而木星绕太阳作圆周运动的中心体是太阳,卫星绕木星作圆周运动的中心体为木星,所以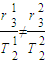 ,故D错误.
,故D错误.
故选AC.
点评:一个物理量能不能求出,我们应该先通过物理规律表示出这个物理量的关系式,再根据题目中已知物理量判断.
开普勒第三定律为: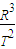 =k,其中我们要清楚k与中心体的质量有关,与环绕体无关.
=k,其中我们要清楚k与中心体的质量有关,与环绕体无关.
某一卫星绕木星作圆周运动,根据万有引力提供向心力,列出等式.
根据题目中已知物理量判断能够求出的物理量.
运用开普勒第三定律求解问题.
解答:解:A、某一卫星绕木星作圆周运动,根据万有引力提供向心力,列出等式:
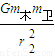 =m卫
=m卫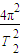 r2
r2m木=
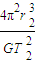
故A正确.
B、由于不知道卫星的质量,所以不能求出木星与卫星间的万有引力,故B错误.
C、太阳与木星间的万有引力提供木星做圆周运动所需要的向心力,
太阳与木星间的万有引力F=m木
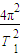 r1=
r1=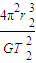 ?
?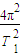 r1=
r1=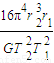
故C正确.
D、根据开普勒第三定律为:
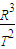 =k,其中我们要清楚k与中心体的质量有关,与环绕体无关.
=k,其中我们要清楚k与中心体的质量有关,与环绕体无关.而木星绕太阳作圆周运动的中心体是太阳,卫星绕木星作圆周运动的中心体为木星,所以
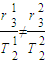 ,故D错误.
,故D错误.故选AC.
点评:一个物理量能不能求出,我们应该先通过物理规律表示出这个物理量的关系式,再根据题目中已知物理量判断.
开普勒第三定律为:
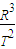 =k,其中我们要清楚k与中心体的质量有关,与环绕体无关.
=k,其中我们要清楚k与中心体的质量有关,与环绕体无关. 
练习册系列答案
相关题目
木星是太阳系中最大的行星,它有众多卫星.观察测出:木星绕太阳作圆周运动的半径为r1、周期为T1;木星的某一卫星绕木星作圆周运动的半径为r2、周期为T2.已知万有引力常量为G,则根据题中给定条件
| A.能求出木星的质量 |
| B.能求出木星与卫星间的万有引力 |
| C.能求出太阳与木星间的万有引力 |
D.可以断定 |
