题目内容
2.甲乙两车从同一地点沿同一方向做直线运动.甲车以4m/s的速度做匀速运动先行出发,2s后乙以1m/s2的加速度做初速度为零的匀加速运动.求:(1)乙车启动后经多长时间追上甲车
(2)在乙车追上甲车前,何时两车相距最远?两车最远的距离是多少?
分析 (1)乙车追上甲车时,抓住位移关系,运用运动学公式求出追及的时间.
(2)两车速度相等前,两车的距离越来越大,速度相等后,两车的距离越来越小,知速度相等时,两车相距最远.
解答 解:(1)设经过t时间乙车追上甲车,有:v1(t+2)=$\frac{1}{2}$at2
代入数据解得:t=4+$4\sqrt{2}$≈11.7s
(2)当两车速度相等时,相距最远,则有:t′=$\frac{{v}_{1}}{a}$=$\frac{4}{1}$=4s
此时甲车的位移为:x1=4×(4+2)m=24m
乙车的位移为:x2=$\frac{1}{2}$at′2=$\frac{1}{2}$×1×16=8m
△x=x1-x2=24-8=16m
答:(1)乙车启动后经过11.7s追上甲车.
(2)在乙车追上甲车前,经过4s相距最远,最远距离为16m.
点评 本题属于运动学中的追及问题,关键是灵活掌握运动学公式,知道在该问题中速度相等时,距离最远.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.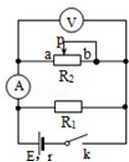 如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )
如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )
 如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )
如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )| A. | 当R2=$\frac{{R}_{1}}{2}$时,R2上获得最大功率 | |
| B. | 当R2=R1时,R2上获得最大功率 | |
| C. | 电压表示数和电流表示数之比逐渐增大 | |
| D. | 电压表示数和电流表示数之比保持不变 |
13.图为“测量匀变速直线运动的加速度”的实验装置示意图.实验步骤如下:
①测得遮光片的宽度为b;两光电门之间的距离为d;
②调整轻滑轮,使细线水平;
③让物块从光电门A的左侧由静止释放,用数字毫秒计分别测出遮光片经过光电门A和光电门B所用的时间△t1和△t2,求出加速度a;
④多次重复步骤③,求a的平均值$\overline{a}$;

回答下列为题:
(1)物块的加速度a可用d、b、△t1,和△t2,表示为a=$\frac{{b}^{2}}{2d}(\frac{1}{△{t}_{2}^{2}}-\frac{1}{△{t}_{1}^{2}})$
(2)(多选题)为减小实验误差,可采取的方法是BC
①测得遮光片的宽度为b;两光电门之间的距离为d;
②调整轻滑轮,使细线水平;
③让物块从光电门A的左侧由静止释放,用数字毫秒计分别测出遮光片经过光电门A和光电门B所用的时间△t1和△t2,求出加速度a;
④多次重复步骤③,求a的平均值$\overline{a}$;

回答下列为题:
(1)物块的加速度a可用d、b、△t1,和△t2,表示为a=$\frac{{b}^{2}}{2d}(\frac{1}{△{t}_{2}^{2}}-\frac{1}{△{t}_{1}^{2}})$
(2)(多选题)为减小实验误差,可采取的方法是BC
| A.增大遮光片宽度b | B.减小遮光片宽度b |
| C.增大两光电门间距d | D.减小两光电门间距d |
10. 有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
 有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )| A. | 电阻R消耗的电功率增大 | B. | 灯L1、L2都能正常发光 | ||
| C. | 原线圈的输入功率减小 | D. | 原、副线圈的电流比减小 |
17.地球同步卫星与地球的白转周期必须相同,若地球由于某种原因白转周期变为12小时,则此情况下的同步卫星与我们现在使用的同步卫星比较,下列说法正确的是( )
| A. | 轨道半径变大,大小变为2倍 | B. | 轨道半径变小,大小变为$\frac{1}{2}$倍 | ||
| C. | 轨道半径变大,大小变为2${\;}^{\frac{2}{3}}$倍 | D. | 轨道半径变小,大小变为($\frac{1}{2}$)${\;}^{\frac{2}{3}}$倍 |
14.以下几种关于质点的说法,你认为正确的是( )
| A. | 只有体积很小或质量很小的物体才可以看作质点 | |
| B. | 只要物体运动得不是很快,物体就可以看作质点 | |
| C. | 研究地球的自转时,可以将地球看作质点 | |
| D. | 物体的大小和形状在所研究的问题中起的作用很小,可以忽略不计时,我们就可以把物体看作质点 |
11.一个质量1kg的石块从阳台上自由下落,1s末到达地面.这个过程( )
| A. | 1s内重力的平均功率是50W | B. | 1s内重力的平均功率是100W | ||
| C. | 落地时重力的瞬时功率是50W | D. | 落地时重力的瞬时功率是100W |

 如图为某物体做直线运动的v-t图象.试分析物体在各段时间内的运动情况并计算各阶段加速度的大小和方向.
如图为某物体做直线运动的v-t图象.试分析物体在各段时间内的运动情况并计算各阶段加速度的大小和方向.