题目内容
16.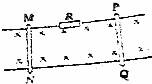 如图所示,两根水平金属导轨置于垂直纸面向里的匀强磁场中,磁场的磁感应强度为B,其中一根导轨中串有一个电阻R,两根金属棒MN、PQ垂直金属导轨放置,每根金属棒长为L,电阻为r,当两根金属棒都以速度v向相反方向运动时,求R上的发热功率.
如图所示,两根水平金属导轨置于垂直纸面向里的匀强磁场中,磁场的磁感应强度为B,其中一根导轨中串有一个电阻R,两根金属棒MN、PQ垂直金属导轨放置,每根金属棒长为L,电阻为r,当两根金属棒都以速度v向相反方向运动时,求R上的发热功率.
分析 两根金属棒以速度v向相反方向运动时都产生感应电动势,两个电动势串联,得到总的感应电动势,再由闭合电路欧姆定律求出电路中电流,即可求得R上的发热功率.
解答 解:两根金属棒产生的感应电动势均为 E=BLv,由右手定则判断知,两棒的感应电动势串联,回路中总的感应电动势为:E总=2E=2BLv
回路中感应电流为:I=$\frac{{E}_{总}}{R+2r}$=$\frac{2BLv}{R+2r}$
R上的发热功率为:P=I2R=$\frac{4{B}^{2}{L}^{2}{v}^{2}R}{(R+2r)^{2}}$
答:R上的发热功率为$\frac{4{B}^{2}{L}^{2}{v}^{2}R}{(R+2r)^{2}}$.
点评 本题是双杆类型,当两杆反向运动时产生感应电动势是串联关系,当两杆同向运动时产生感应电动势会反接.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.关于电场线下列说法中正确的是( )
| A. | 电场线平行且间距相等的电场是匀强电场 | |
| B. | 电场线是首尾相连的闭合曲线 | |
| C. | 电场线是形象描述电场分布情况的实际存在于电场的曲线 | |
| D. | 电场的两条电场线有可能相交 |
11. 如图所示,一个由三条边围成的矩形金属框内匀强磁场,磁感应强度为B,有一根垂直于磁场和金属框的电阻棒,其在金属框内的电阻为R,在金属框内的长度为L,矩形金属框的电阻不计.电阻棒与金属框的摩擦不计,在大小和方向恒定的外力F的作用下,电阻棒以速度v匀速向右运动,拉力外力F与速度v、长度L、磁感应强度B、电阻R之间的关系数据如下表:
如图所示,一个由三条边围成的矩形金属框内匀强磁场,磁感应强度为B,有一根垂直于磁场和金属框的电阻棒,其在金属框内的电阻为R,在金属框内的长度为L,矩形金属框的电阻不计.电阻棒与金属框的摩擦不计,在大小和方向恒定的外力F的作用下,电阻棒以速度v匀速向右运动,拉力外力F与速度v、长度L、磁感应强度B、电阻R之间的关系数据如下表:
(1)拉力外力F与速度v、长度L、磁感应强度B、电阻R之间的关系的表达式为F=k$\frac{{B}^{2}{L}^{2}v}{R}$;其中k=1N•Ω/(T2•m3•s-1)(带单位).
(2)在速度v、长度L、磁感应强度B一定时,拉力外力F与电阻R之间的关系可用图象是的图线b表示.
(3)若拉力为0.04N,磁感应强度为0.4T,电阻为0.2Ω,长度为0.2m,则电阻棒匀速运动时速度为1.25m/s.
 如图所示,一个由三条边围成的矩形金属框内匀强磁场,磁感应强度为B,有一根垂直于磁场和金属框的电阻棒,其在金属框内的电阻为R,在金属框内的长度为L,矩形金属框的电阻不计.电阻棒与金属框的摩擦不计,在大小和方向恒定的外力F的作用下,电阻棒以速度v匀速向右运动,拉力外力F与速度v、长度L、磁感应强度B、电阻R之间的关系数据如下表:
如图所示,一个由三条边围成的矩形金属框内匀强磁场,磁感应强度为B,有一根垂直于磁场和金属框的电阻棒,其在金属框内的电阻为R,在金属框内的长度为L,矩形金属框的电阻不计.电阻棒与金属框的摩擦不计,在大小和方向恒定的外力F的作用下,电阻棒以速度v匀速向右运动,拉力外力F与速度v、长度L、磁感应强度B、电阻R之间的关系数据如下表:| 长度L/m | 磁感应强度B/T | 速度v/(m•s-1) | 电阻R/Ω | 拉力F/N |
| 0.1 | 0.2 | 1 | 4 | 10-3 |
| 0.1 | 0.2 | 1 | 2 | 2×10-3 |
| 0.1 | 0.6 | 1 | 4 | 9×10-3 |
| 0.2 | 0.6 | 1 | 4 | 3.6×10-3 |
| 0.1 | 0.2 | 4 | 1 | 1.6×10-3 |
(2)在速度v、长度L、磁感应强度B一定时,拉力外力F与电阻R之间的关系可用图象是的图线b表示.

(3)若拉力为0.04N,磁感应强度为0.4T,电阻为0.2Ω,长度为0.2m,则电阻棒匀速运动时速度为1.25m/s.
1.以下说法正确的是( )
| A. | 物体速度越小,加速度一定越小 | |
| B. | 物体在某时刻速度为零,其加速度也一定为零 | |
| C. | 只要物体有加速度,其速度一定是越来越大 | |
| D. | 物体速度变化越慢,加速度一定越小 |
8.质点从斜面底端以一定的初速度沿斜面匀速上滑,第1s内上滑2m,最后1s内上滑1m,刚好到达斜面顶端.则质点上滑的加速度大小和斜面的长度为( )
| A. | 2m/s2 ,4m | B. | 4m/s2,2.25m | C. | 2m/s2,2.25m | D. | 4m/s2 ,4m |
9. 如图所示,均匀轻金属棒ab位于桌面上方的正交电磁场中,电场E、磁场B方向如图所示,当金属棒ab从水平状态由静止开始自由下落时(不计空气阻力),a、b两端落到桌面的先后顺序是( )
如图所示,均匀轻金属棒ab位于桌面上方的正交电磁场中,电场E、磁场B方向如图所示,当金属棒ab从水平状态由静止开始自由下落时(不计空气阻力),a、b两端落到桌面的先后顺序是( )
 如图所示,均匀轻金属棒ab位于桌面上方的正交电磁场中,电场E、磁场B方向如图所示,当金属棒ab从水平状态由静止开始自由下落时(不计空气阻力),a、b两端落到桌面的先后顺序是( )
如图所示,均匀轻金属棒ab位于桌面上方的正交电磁场中,电场E、磁场B方向如图所示,当金属棒ab从水平状态由静止开始自由下落时(不计空气阻力),a、b两端落到桌面的先后顺序是( )| A. | a、b同时 | B. | a 先于b | C. | b先于a | D. | 无法确定 |
 如图所示,长木板B静止在光滑的水平面上,物块C放在长木板的右端,B的质量为4kg,C和木板间的动摩擦因数为0.2,C可以看成质点,长木板足够长,物块A在长木板的右侧以速度v0=8m/s向右运动并与长木板相碰,碰后A的速度为2m/s,方向不变,A的质量为2kg,g取10m/s2,求:
如图所示,长木板B静止在光滑的水平面上,物块C放在长木板的右端,B的质量为4kg,C和木板间的动摩擦因数为0.2,C可以看成质点,长木板足够长,物块A在长木板的右侧以速度v0=8m/s向右运动并与长木板相碰,碰后A的速度为2m/s,方向不变,A的质量为2kg,g取10m/s2,求:
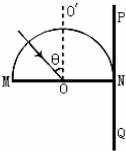 半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ=30°角射向O点,已知有两束折射率n1=$\sqrt{2}$,n2=$\sqrt{3}$的光束,因而光屏两个光斑.
半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ=30°角射向O点,已知有两束折射率n1=$\sqrt{2}$,n2=$\sqrt{3}$的光束,因而光屏两个光斑.