题目内容
4. 如图所示,A球放在一个倾角为30°的固定的光滑斜面上,A、B两小球由绕过轻质定滑轮的细线相连,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚好伸直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知B、C的质量均为m,重力加速度g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.已知弹簧拉伸和压缩形变量相同时,其储存的弹性势能相同,试求:
如图所示,A球放在一个倾角为30°的固定的光滑斜面上,A、B两小球由绕过轻质定滑轮的细线相连,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚好伸直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知B、C的质量均为m,重力加速度g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.已知弹簧拉伸和压缩形变量相同时,其储存的弹性势能相同,试求:(1)A球的质量mA多大?
(2)A球能获得的最大速度是多少?
分析 (1)C球刚离开地面时,弹簧的弹力等于C的重力,根据牛顿第二定律知B的加速度为零,B、C加速度相同,分别对B、A受力分析,列出平衡方程,可以求出A的质量.
(2)对B、C组成的系统由动能定理可以求出最大速度.
解答 解:(1)当A所受合力为零时,速度最大,此时:aA=aB=aC=0,
此时C刚离开地面时,由平衡条件得:
对C:kx2=mg,
对B:T-kx2-mg=0,
对A:mAgsin30°-T=0,
解得:mA=4m;
(2)开始时系统静止,且线上无拉力,
对B有:kx1=mg,
解得:x1=x2=$\frac{mg}{k}$,
则从释放A至C刚离开地面过程中,弹性势能变化量为零,此过程中由动能定理得:
mAg(x1+x2)sin30°-mg(x1+x2)=$\frac{1}{2}$(mA+m)v2-0,解得:v=2g$\sqrt{\frac{m}{5k}}$;
答:(1)A球的质量mA为4m.
(2)A球能获得的最大速度是2g$\sqrt{\frac{m}{5k}}$.
点评 本题关键是对三个小球进行受力分析,确定出它们的运动状态,再结合平衡条件和动能定理即可正确解题.

练习册系列答案
相关题目
15.关于作用力和反作用力,下列说法中正确的是( )
| A. | 只有相互作用的物体都静止时,作用力和反作用力大小才相等 | |
| B. | 摩擦力的反作用力可以是弹力 | |
| C. | 作用力和反作用力可以相互平衡 | |
| D. | 作用力和反作用力的产生无先后之分 |
12.2013年12月,“玉兔号”月球车被送上月球,关于其登月前后惯性的变化,下列说法正确的是( )
| A. | 不变 | B. | 消失 | C. | 减小 | D. | 增大 |
13. 如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )
如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )
 如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )
如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )| A. | 带电粒子每运动一周被加速一次 | |
| B. | P1P2=P2P3 | |
| C. | 粒子能达到的最大速度与D形盒的尺寸无关 | |
| D. | 加速电场的方向需要做周期性的变化 |
 如图(1)所示,平行金属板板间距离为d,紧靠金属板右端竖直放置一绝缘挡板,挡板上正对平行金属板中线处有一小孔,挡板右侧距挡板L处竖直放置一荧光屏,荧光屏与金属板中线相交于O点,整个装置处在垂直纸面向里的匀强磁场中,磁感应强度为B.现在两金属板间加一按图(2)所示规律变化的电压,并从t=0时刻开始,有大量的、各种不同速率的相同离子从金属板左侧沿中线连续不断的射入,已知这些离子通过金属板所用的时间极短,以至于每个离子通过金属板的过程中,板间电场可认为是恒定的.受电、磁场的影响,这些离子有的被挡板挡住,有的能沿直线通过挡板上的小孔而进入挡板右侧的区域,若从小孔射出的离子刚好能全部打在荧光屏上(不计离子重力).
如图(1)所示,平行金属板板间距离为d,紧靠金属板右端竖直放置一绝缘挡板,挡板上正对平行金属板中线处有一小孔,挡板右侧距挡板L处竖直放置一荧光屏,荧光屏与金属板中线相交于O点,整个装置处在垂直纸面向里的匀强磁场中,磁感应强度为B.现在两金属板间加一按图(2)所示规律变化的电压,并从t=0时刻开始,有大量的、各种不同速率的相同离子从金属板左侧沿中线连续不断的射入,已知这些离子通过金属板所用的时间极短,以至于每个离子通过金属板的过程中,板间电场可认为是恒定的.受电、磁场的影响,这些离子有的被挡板挡住,有的能沿直线通过挡板上的小孔而进入挡板右侧的区域,若从小孔射出的离子刚好能全部打在荧光屏上(不计离子重力).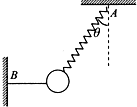 如图所示,轻质弹簧一端固定于A点,另一端悬挂一质量m=0.4kg的小球,并通过水平轻绳固定于B点,弹簧的轴线与竖直方向的夹角θ=37°,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,轻质弹簧一端固定于A点,另一端悬挂一质量m=0.4kg的小球,并通过水平轻绳固定于B点,弹簧的轴线与竖直方向的夹角θ=37°,g取10m/s2,sin37°=0.6,cos37°=0.8,求: 如图所示,有四块相同的滑块叠放起来置于水平桌面上,通过细绳和定滑轮相互联接起来.如果所有的接触面间的摩擦系数均为μ,每一滑块的质量均为m,不计滑轮的摩擦.那么要拉动最上面一块滑块至少需要多大的水平拉力?如果有n块这样的滑块叠放起来,那么要拉动最上面的滑块,至少需多大的拉力?
如图所示,有四块相同的滑块叠放起来置于水平桌面上,通过细绳和定滑轮相互联接起来.如果所有的接触面间的摩擦系数均为μ,每一滑块的质量均为m,不计滑轮的摩擦.那么要拉动最上面一块滑块至少需要多大的水平拉力?如果有n块这样的滑块叠放起来,那么要拉动最上面的滑块,至少需多大的拉力?