题目内容
3.水平放置的平行板电容器的电容为C,板间距离为d,极板足够长,当其带电荷量为Q时,沿两板中央水平射入的带电荷量为q的微粒恰好做匀速直线运动.若使电容器电荷量增大一倍,则该带电微粒落到某一极板上所需时间为多少?分析 由平行板电容器的场强公式E=$\frac{U}{d}$、Q=CU整理得到场强与极板带电量之间的关系,结合粒子第一个过程做匀速运动可以整理得到重力得表达式,代入粒子的第二个运动过程,即类平抛运动解出此题.
解答 解:平行板电容器间的场强:E=$\frac{U}{d}$,
电热器所带电荷量:Q=CU,
整理得:E=$\frac{Q}{Cd}$,
粒子沿两板中央水平射入的带电荷量为q的微粒恰好做匀速直线运动,
由平衡条件得:qE=mg
若使电容器带电荷量为2Q,极板间的场强为:E2=2E,
所以粒子所受的合力竖直向上:F合=qE2-mg=qE=mg,
由牛顿第二定律得:mg=ma,解得:a=g,
粒子在极板间做类平抛运动,水平方向匀速直线运动,
竖直向上做初速度为零、加速度大小为:a=g的匀加速运动.
竖直方向:$\frac{d}{2}$=$\frac{1}{2}$at2,解得:t=$\sqrt{\frac{d}{g}}$;
答:该带电微粒落到某一极板上所需时间为:$\sqrt{\frac{d}{g}}$.
点评 注意类平抛运动过程水平方向的运动与竖直方向的运动具有等时性,然后分别应用匀速运动规律和初速度为零匀加速直线运动规律解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.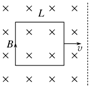 如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
 如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )| A. | 若v1>v2,则拉力F1>F2 | |
| B. | 若v1>v2,则通过导线框截面的电荷量q1>q2 | |
| C. | 若v1>v2,则拉力的功率P1=2P2 | |
| D. | 若v1>v2,则线框中产生的热量Q1=2Q2 |
18. 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )
 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )| A. | 200 V/m | B. | 200 $\sqrt{3}$ V/m | C. | 100 V/m | D. | 100 $\sqrt{3}$ V/m |
8.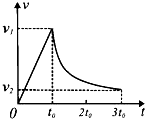 在“跨越-2015•朱日和”系列军事演习中,某部伞兵进行了飞行跳伞演习,该伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地,他的速度随时间变化的规律如图所示,其中0~t0内是直线,下列结论正确的是( )
在“跨越-2015•朱日和”系列军事演习中,某部伞兵进行了飞行跳伞演习,该伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地,他的速度随时间变化的规律如图所示,其中0~t0内是直线,下列结论正确的是( )
 在“跨越-2015•朱日和”系列军事演习中,某部伞兵进行了飞行跳伞演习,该伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地,他的速度随时间变化的规律如图所示,其中0~t0内是直线,下列结论正确的是( )
在“跨越-2015•朱日和”系列军事演习中,某部伞兵进行了飞行跳伞演习,该伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地,他的速度随时间变化的规律如图所示,其中0~t0内是直线,下列结论正确的是( )| A. | 伞兵在0~t0时间内加速度不变,在t0~3t0时间内加速度增大 | |
| B. | 伞兵在t0~3t0时间内,平均速度为$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| C. | 降落伞打开后,降落伞和伞兵所受的阻力越来越小 | |
| D. | 降落伞打开后,降落伞和伞兵所受的阻力大小恒定 |
15. 如图,水平正对放置的两块足够大的矩形金属板,分别与一恒压直流电源(图中未画出)的两极相连,M、N是两极板的中心.若把一带电微粒在两板之间a点从静止释放,微粒将恰好保持静止.现将两板绕过M、N且垂直于纸面的轴逆时针旋转一个小角度θ后,再由a点从静止释放一这样的微粒,该微粒将( )
如图,水平正对放置的两块足够大的矩形金属板,分别与一恒压直流电源(图中未画出)的两极相连,M、N是两极板的中心.若把一带电微粒在两板之间a点从静止释放,微粒将恰好保持静止.现将两板绕过M、N且垂直于纸面的轴逆时针旋转一个小角度θ后,再由a点从静止释放一这样的微粒,该微粒将( )
 如图,水平正对放置的两块足够大的矩形金属板,分别与一恒压直流电源(图中未画出)的两极相连,M、N是两极板的中心.若把一带电微粒在两板之间a点从静止释放,微粒将恰好保持静止.现将两板绕过M、N且垂直于纸面的轴逆时针旋转一个小角度θ后,再由a点从静止释放一这样的微粒,该微粒将( )
如图,水平正对放置的两块足够大的矩形金属板,分别与一恒压直流电源(图中未画出)的两极相连,M、N是两极板的中心.若把一带电微粒在两板之间a点从静止释放,微粒将恰好保持静止.现将两板绕过M、N且垂直于纸面的轴逆时针旋转一个小角度θ后,再由a点从静止释放一这样的微粒,该微粒将( )| A. | 仍然保持静止 | |
| B. | 靠近电势较低的电极板 | |
| C. | 以 a=g(1-cosθ) 的竖直加速度加速(g表示重力加速度) | |
| D. | 以 a=gtanθ 的水平加速度加速(g表示重力加速度) |
13.有两个共点力,一个力的大小是5N,另一个力的大小是2N,它们合力的大小可能是( )
| A. | 10 N | B. | 7 N | C. | 5 N | D. | 2N |

 如图所示,在竖直放置的足够大的铅屏A的右表面上贴着β 射线(即电子)放射源P,已知射线实质为高速电子流,放射源放出β 粒子的速度为v0.足够大的荧光屏M与铅屏A平行放置,相距为d,其间有水平向左的匀强电场,电场强度大小为E.已知电子电量为e,电子质量为m.求:
如图所示,在竖直放置的足够大的铅屏A的右表面上贴着β 射线(即电子)放射源P,已知射线实质为高速电子流,放射源放出β 粒子的速度为v0.足够大的荧光屏M与铅屏A平行放置,相距为d,其间有水平向左的匀强电场,电场强度大小为E.已知电子电量为e,电子质量为m.求: 如图所示,竖直平面直角坐标系中,一半径为R的绝缘光滑管道位于其中,管道圆心坐标为(0,R),其下端点与x轴相切与坐标原点,其上端点与y轴交于C点,坐标为(0,2R).在第二象限内,存在水平向右、范围足够大的匀强电场,电场强度大小为E1=$\frac{\sqrt{3}mg}{3q}$,在x≥R,y≥0范围内,有水平向左,范围足够大的匀强电场,电场强度大小为E1=$\frac{mg}{q}$.现有一与x轴正方向夹角为45°,足够长的绝缘斜面位于第一象限的电场中,斜面底端坐标为(R,0),x轴上0≤x≤R范围内是水平光滑轨道,左端与管道下端相切,右端与斜面底端平滑连接,有一质量为m,带电量为+q的小球,从静止开始,由斜面上某点A下滑,通过水平光滑轨道(不计转角处能量损失),从管道下端点B进入管道(小球直径略小于管道内径,不计小球的电量损失)(已知重力加速度为g).试求:
如图所示,竖直平面直角坐标系中,一半径为R的绝缘光滑管道位于其中,管道圆心坐标为(0,R),其下端点与x轴相切与坐标原点,其上端点与y轴交于C点,坐标为(0,2R).在第二象限内,存在水平向右、范围足够大的匀强电场,电场强度大小为E1=$\frac{\sqrt{3}mg}{3q}$,在x≥R,y≥0范围内,有水平向左,范围足够大的匀强电场,电场强度大小为E1=$\frac{mg}{q}$.现有一与x轴正方向夹角为45°,足够长的绝缘斜面位于第一象限的电场中,斜面底端坐标为(R,0),x轴上0≤x≤R范围内是水平光滑轨道,左端与管道下端相切,右端与斜面底端平滑连接,有一质量为m,带电量为+q的小球,从静止开始,由斜面上某点A下滑,通过水平光滑轨道(不计转角处能量损失),从管道下端点B进入管道(小球直径略小于管道内径,不计小球的电量损失)(已知重力加速度为g).试求: