题目内容
11. 如图所示,质量为mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量为mA=2kg的物体A.一颗质量为m0=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=200m/s,则:
如图所示,质量为mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量为mA=2kg的物体A.一颗质量为m0=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=200m/s,则:①子弹与物块A相互作用后,物块A的速度vA多大?若平板车B足够长,A、B相互作用后,A、B的共同速度vB多大?
②已知A、B之间的动摩擦因数为μ=0.25,g取10m/s2,为使物块A不滑离小车B,小车的长度L至少为多少?
分析 (1)子弹穿过A的过程中水平方向的动量守恒,当子弹射出A后,A获得速度;随后A做匀减速直线运动,平板车B做匀加速直线运动,当A、B速度相同时,平板车的速度最大,对A、B组成的系统研究,根据动量守恒定律求出共同的速度.
(2)A在B上发生相对滑动时产生内能,根据能量守恒定律即可求出.
解答 解:(1)对子弹和物体A组成的系统研究,水平方向在碰撞的瞬间动量守恒,选取向右为正方向,根据动量守恒定律得:
m0v0=m0v+mAvA
代入数据得:0.01×600=0.01×200+2vA
解得:vA=2m/s.
对A、B组成的系统研究,根据动量守恒定律得:
mAvA=(mA+mB)vB
代入数据解得:vB=1m/s.
(2)根据能量守恒定律得,物体A在B上相对滑动时,产生的内能为:
$Q=\frac{1}{2}{m}_{A}{{v}_{A}}^{2}-\frac{1}{2}({m}_{A}+{m}_{B}){{v}_{B}}^{2}$=$\frac{1}{2}×2×4-\frac{1}{2}×4×1$=2 J.
该过程中:μmAgL=Q.
联立得:L=0.4m
答:①子弹与物块A相互作用后,物块A的速度vA是2m/s;若平板车B足够长,A、B相互作用后,A、B的共同速度vB是1m/s;
②已知A、B之间的动摩擦因数为μ=0.25,g取10m/s2,为使物块A不滑离小车B,小车的长度L至少为0.4m.
点评 本题综合考查了动量守恒定律和能量守恒定律,综合性较强,是道好题.运用动量守恒定律解题时,关键要合理地选择研究的系统.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
1. 如图所示为牵引力F和车速倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,设其最大车速为30m/s,则正确的是( )
如图所示为牵引力F和车速倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,设其最大车速为30m/s,则正确的是( )
 如图所示为牵引力F和车速倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,设其最大车速为30m/s,则正确的是( )
如图所示为牵引力F和车速倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,设其最大车速为30m/s,则正确的是( )| A. | 汽车所受阻力为2×103N | B. | 汽车车速为15m/s,功率为3×104W | ||
| C. | 汽车匀加速的加速度为3m/s2 | D. | 汽车匀加速所需时间为5s |
2.下列说法中正确的是( )
| A. | 一切波都能发生干涉、衍射现象 | |
| B. | 只有两列横波相遇时才能发生干涉 | |
| C. | 在障碍物的后面可以听到前面人说话的声音是衍射现象 | |
| D. | 发生多普勒效应时,观察者接收的频率发生了变化,是波源的频率变化的缘故 |
19.如图所示,为一物体运动的速度一时间图象,下列说法正确的是( )


| A. | 物体在0~1s内,a=4m/s2 | |
| B. | 物体在2~3s内的加速度与在3~4s内的加速度相同 | |
| C. | 物体在3~4s秒内的加速度与4~5s内的加速度相同 | |
| D. | 物体在5s内总位移为4m |
6.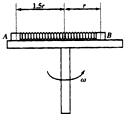 如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设最大静摩擦力等于滑动摩擦力,当B受到的摩擦力为零时,转台转动的角速度为( )
如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设最大静摩擦力等于滑动摩擦力,当B受到的摩擦力为零时,转台转动的角速度为( )
 如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设最大静摩擦力等于滑动摩擦力,当B受到的摩擦力为零时,转台转动的角速度为( )
如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设最大静摩擦力等于滑动摩擦力,当B受到的摩擦力为零时,转台转动的角速度为( )| A. | $\sqrt{\frac{k}{m}}$ | B. | $\sqrt{\frac{k}{2m}}$ | C. | $\sqrt{\frac{k}{2m}+\frac{μg}{2r}}$ | D. | $\sqrt{\frac{2k}{3m}+\frac{2μg}{3r}}$ |
9.下列说法正确的是( )
| A. | 带电粒子在匀强磁场中做匀速圆周运动的周期T会随入射速度的增大而增大 | |
| B. | 洛仑磁力既不能改变粒子的动能,也不能改变粒子的速度 | |
| C. | 放在匀强电场中各处的同一电荷,所受电场力的大小和方向处处相同 | |
| D. | 放在匀强磁场中各处的同一通电导线,所受磁场力的大小和方向处处相同 |
6. 如图所示电路中AB两端加交流电压u=141sin157tV时,小灯泡发光,若AB间电压换为如下四种情况时(小灯泡都没有被烧毁),可以使小灯亮度增加的是( )
如图所示电路中AB两端加交流电压u=141sin157tV时,小灯泡发光,若AB间电压换为如下四种情况时(小灯泡都没有被烧毁),可以使小灯亮度增加的是( )
 如图所示电路中AB两端加交流电压u=141sin157tV时,小灯泡发光,若AB间电压换为如下四种情况时(小灯泡都没有被烧毁),可以使小灯亮度增加的是( )
如图所示电路中AB两端加交流电压u=141sin157tV时,小灯泡发光,若AB间电压换为如下四种情况时(小灯泡都没有被烧毁),可以使小灯亮度增加的是( )| A. | 交流电压u=141sin314tV | B. | 直流电压100V | ||
| C. | 交流电压u=141sin100tV | D. | 直流电压141V |
7.有关安培力和洛伦兹力的说法,以下正确的是( )
| A. | 通电直导线在匀强磁场中不一定受到安培力的作用 | |
| B. | 运动电荷在磁场中一定受到洛伦兹力 | |
| C. | 运动电荷在匀强磁场中受到的洛伦兹力对电荷不做功 | |
| D. | 通电直导线在匀强磁场中受到的安培力可能与磁场方向平行 |
 如图所示,有质量为m1=2kg、m2=3kg的两个物体放置于水平地面上,它们与地面的动摩擦因数分别为μ1=0.2,μ2=0.1.用F=22N的水平推力推两物体,使它们由静止开始一起向右运动,经过一段时间后撤去力F,当两物块都停止运动后,相距△x=6.75m.已知重力加速度g=10m/s2,求力F作用的时间t?
如图所示,有质量为m1=2kg、m2=3kg的两个物体放置于水平地面上,它们与地面的动摩擦因数分别为μ1=0.2,μ2=0.1.用F=22N的水平推力推两物体,使它们由静止开始一起向右运动,经过一段时间后撤去力F,当两物块都停止运动后,相距△x=6.75m.已知重力加速度g=10m/s2,求力F作用的时间t?