题目内容
6. 如图所示,物体的质量为5kg,两根轻质细绳AB和AC的一端连接于竖直墙上的B、C两点,另一端系于物体上A点,(已知$\sqrt{6}$=2.449、$\sqrt{2}$=1.414、$\sqrt{3}$=1.732,g=10m/s2),求:
如图所示,物体的质量为5kg,两根轻质细绳AB和AC的一端连接于竖直墙上的B、C两点,另一端系于物体上A点,(已知$\sqrt{6}$=2.449、$\sqrt{2}$=1.414、$\sqrt{3}$=1.732,g=10m/s2),求:(1)若在物体上施加一外力F,使AB、AC伸直,则F的最小值为多大?
(2)若在物体上施加一个方向与水平成θ=45°的拉力F,要使AB、AC绳都能伸直,求拉力F的大小范围?(结果均保留三位有效数字)
分析 (1)由图可知,若两绳均伸直,则AB拉力可以提供向上的效果,而AC只能提供向下拉的效果,故当AC伸直但没有拉力时,此时有最小值,再根据几何关系即可求得最小值;
(2)对小球分析,明确AB和BC分别处于伸直但没有弹力的状态下为临界条件,分别作出平行四边形,由几何关系进行分析求解.
解答  解:(1)当AC恰好伸直但没有拉力时,此时A受重力、AB的拉力以及外力F,如图所示,当拉力方向与AB垂直时,拉力最小,最小值为:F'=mgcos30°=50×$\frac{\sqrt{3}}{2}$=25$\sqrt{3}$N;
解:(1)当AC恰好伸直但没有拉力时,此时A受重力、AB的拉力以及外力F,如图所示,当拉力方向与AB垂直时,拉力最小,最小值为:F'=mgcos30°=50×$\frac{\sqrt{3}}{2}$=25$\sqrt{3}$N;
(2)作出物体A受力如图1所示,由平衡条件
Fy=Fsin45°+F1sinθ-mg-F2sin30°=0…①
Fx=Fcos45°-F2cos30°-F1cos30°=0…②
由当F较小时,绳AC中F2=0,即F和F1 的合力与重力mg平衡,由图2所示;
由几何关系解得:Fmin=44.8N
当F较大时,绳AB中张力F1=0,F和F2 的合力与重力mg平衡,如图4所示,
由几何关系解得:Fmax=167N
故拉力F的范围为;44.8N-167N.
答:(1)若在物体上施加一外力F,使AB、AC伸直,则F的最小值为25$\sqrt{3}$N;
(2)拉力F的大小范围为44.8N-167N.


点评 本题关键是对小球受力分析,列平衡方程,然后找出最大和最小两种临界情况讨论,本题的难度较大,要求学生有较高的数学知识的应用能力,注意在求解拉力的范围时用到的几何关系为正弦定理,注意图3中重力所对夹角为105°,而图4中重力所对夹角为15°;sin105°=$\frac{\sqrt{6}+\sqrt{2}}{4}$,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{2}$.正弦定理为:$\frac{a}{sinα}=\frac{b}{sinβ}=\frac{c}{sinγ}$.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案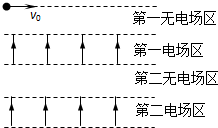 一个质量为m、电荷量为+q的小球以初速度v0水平抛出,在小球经过的竖直平面内,存在着若干个如图所示的无电场区和有理想上下边界的匀强电场区,两区域相互间隔、竖直高度相等,电场区水平方向无限长,已知每一电场区的场强大小相等、方向均竖直向上,不计空气阻力,下列说法正确的是( )
一个质量为m、电荷量为+q的小球以初速度v0水平抛出,在小球经过的竖直平面内,存在着若干个如图所示的无电场区和有理想上下边界的匀强电场区,两区域相互间隔、竖直高度相等,电场区水平方向无限长,已知每一电场区的场强大小相等、方向均竖直向上,不计空气阻力,下列说法正确的是( )| A. | 若场强大小等于$\frac{mg}{q}$,则小球经过每一电场区的时间均相同 | |
| B. | 若场强大小等于$\frac{mg}{q}$,则小球经过每一电场区都做直线运动 | |
| C. | 若场强大小等于$\frac{2mg}{q}$,则小球经过每一无电场区的时间均相同 | |
| D. | 无论场强大小如何,小球通过所有无电场区的时间均相同 |
 功率可调的直流电动机线圈内阻恒为2Ω,接在电路中的A、B间,如图,电源的电动势为6V,内阻为2Ω,下列说法正确的是( )
功率可调的直流电动机线圈内阻恒为2Ω,接在电路中的A、B间,如图,电源的电动势为6V,内阻为2Ω,下列说法正确的是( )| A. | 电动机输出最大功率为2.25W | |
| B. | 电源的最大输出功率为4.5W | |
| C. | 电动机输出最大功率时电源输出功率也最大 | |
| D. | 若将电动机改为范围足够大的滑动变阻器,电源可输出得最大功率为4.5W |
 如图所示,三个质量相同,带电荷量分别为+q、-q和0的小液滴a、b、c,从竖直放置的两板中间上方由静止释放,最后从两板间穿过,轨迹如图所示,则在穿过极板的过程中( )
如图所示,三个质量相同,带电荷量分别为+q、-q和0的小液滴a、b、c,从竖直放置的两板中间上方由静止释放,最后从两板间穿过,轨迹如图所示,则在穿过极板的过程中( )| A. | 三者动能的增量相同 | |
| B. | 电场力对液滴a、b做的功相同 | |
| C. | 液滴a电势能的增加量等于液滴b电势能的减小量 | |
| D. | 重力对三者做的功相同 |
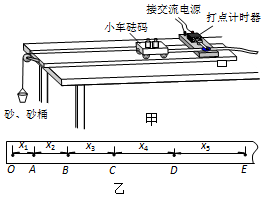
 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=2 m/s | B. | vc=3 m/s | ||
| C. | xde=3 m | D. | 从d到e所用时间为4 s |
| A. | 水平位移 | B. | 下落高度 | ||
| C. | 落地时速度的大小和方向 | D. | 落地时位移的大小和方向 |