题目内容
16.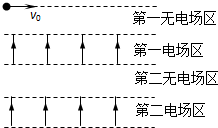 一个质量为m、电荷量为+q的小球以初速度v0水平抛出,在小球经过的竖直平面内,存在着若干个如图所示的无电场区和有理想上下边界的匀强电场区,两区域相互间隔、竖直高度相等,电场区水平方向无限长,已知每一电场区的场强大小相等、方向均竖直向上,不计空气阻力,下列说法正确的是( )
一个质量为m、电荷量为+q的小球以初速度v0水平抛出,在小球经过的竖直平面内,存在着若干个如图所示的无电场区和有理想上下边界的匀强电场区,两区域相互间隔、竖直高度相等,电场区水平方向无限长,已知每一电场区的场强大小相等、方向均竖直向上,不计空气阻力,下列说法正确的是( )| A. | 若场强大小等于$\frac{mg}{q}$,则小球经过每一电场区的时间均相同 | |
| B. | 若场强大小等于$\frac{mg}{q}$,则小球经过每一电场区都做直线运动 | |
| C. | 若场强大小等于$\frac{2mg}{q}$,则小球经过每一无电场区的时间均相同 | |
| D. | 无论场强大小如何,小球通过所有无电场区的时间均相同 |
分析 将小球的运动沿着水平方向和竖直方向正交分解,其水平方向不受外力,做匀速直线运动,竖直方向在无电场区做匀加速运动,有电场区也做匀变速运动,但加速度不同,运用速度时间关系公式分析,可以得到小球在竖直方向的运动规律.
解答 解:A、将小球的运动沿着水平方向和竖直方向正交分解,水平方向不受外力,以v0做匀速直线运动;竖直方向上,在无电场区只受重力,加速度为g,竖直向下,有电场区除重力外,还受到向上的恒定的电场力作用,加速度的大小和方向取决于合力的大小和方向.
当场强大小等于$\frac{mg}{q}$时,电场力等于mg,故在电场区小球所受的合力为零,在无电场区小球匀加速运动,故经过每个电场区,小球的速度均不等,因而小球经过每一无电场区的时间均不相等,故A错误;
B、当场强大小等于$\frac{mg}{q}$时,电场力等于mg,方向相反,则小球的合力为零,所以小球经过每一电场区都做匀速直线运动,故B正确.
C、若场强大小等于$\frac{2mg}{q}$时,电场力等于2mg,故在电场区小球所受的合力大小等于mg,方向竖直向上,加速度大小等于g,方向竖直向上,根据运动学公式,有
经过第一个无电场区 y=$\frac{1}{2}$gt12,v1=gt1
经过第一个电场区 y=v1t-$\frac{1}{2}$gt22
v2=v1-gt2
联立解得 t1=t2,v2=0,接下来小球的运动重复前面的过程,即每次通过无电场区都是自由落体运动,每次通过电场区都是末速度为零匀减速直线运动,可知,小球经过每一无电场区的时间均相同.故C正确;
D、通过前面的分析可知,物体通过每个无电场区的初速度不一定相同,所以,通过电场的时间不同;故D错误;
故选:BC.
点评 本题是带电粒子在电场中运动的问题,将小球的运动沿水平方向和竖直方向正交分解后,对于竖直方向的运动,关键是找出小球的运动的一般规律,然后分析计算.

| A. | 初速度为6m/s | B. | 加速度为1m/s2 | ||
| C. | 前4 s的位移是8 m | D. | 前4 s的路程是8 m |
 如图所示,两物块A、B套在水平粗糙的CD杆上,并用不可伸长的轻绳连接,整个装置能绕过CD中点的轴OO1转动,已知A的质量比B大,物块与杆的动摩擦因数均为μ,且到轴OO1的距离相等.开始时绳子处于自然长度(绳子恰好伸直但无弹力),现让该装置由静止开始转动,使转速缓慢增大直到两者打滑为止,则下列说法中正确的是( )
如图所示,两物块A、B套在水平粗糙的CD杆上,并用不可伸长的轻绳连接,整个装置能绕过CD中点的轴OO1转动,已知A的质量比B大,物块与杆的动摩擦因数均为μ,且到轴OO1的距离相等.开始时绳子处于自然长度(绳子恰好伸直但无弹力),现让该装置由静止开始转动,使转速缓慢增大直到两者打滑为止,则下列说法中正确的是( )| A. | A受到的静摩擦力先增大后减小 | |
| B. | B受到的静摩擦力先增大后减小再增大 | |
| C. | 在未打滑前,两球受摩擦力的方向可能相同 | |
| D. | 随着角速度的增大,两球向右、向左打滑的可能性都存在 |
 如图所示,一带电粒子从平行带电金属板(平行板电容器)左侧中点垂直于电场线以速度v0射入电场中,恰好能从下板边缘以速率v飞出电场.若其他条件不变,将上、下两个极板同时向上、下两侧平移相同的距离(使板间距离适当增大一些),仍使该粒子从两板左侧中点垂直于电场线以速度v0射入电场中,则以下说法正确的是(不计粒子重力)( )
如图所示,一带电粒子从平行带电金属板(平行板电容器)左侧中点垂直于电场线以速度v0射入电场中,恰好能从下板边缘以速率v飞出电场.若其他条件不变,将上、下两个极板同时向上、下两侧平移相同的距离(使板间距离适当增大一些),仍使该粒子从两板左侧中点垂直于电场线以速度v0射入电场中,则以下说法正确的是(不计粒子重力)( )| A. | 粒子将打在下极板上 | |
| B. | 粒子仍能从下板边缘以速率v飞出电场 | |
| C. | 粒子仍能飞出电场,且飞出电场时的速率仍为v | |
| D. | 粒子仍能飞出电场,且飞出电场时的速率大于v |
(1)在研究物体的“加速度、作用力和质量”三个物理量的关系时,我们用实验研究了小车“在质量一定的情况下,加速度和作用力的关系”;又研究了“在作用力一定的情况下,加速度和质量之间的关系”.这种研究物理问题的科学方法是B
A.建立理想模型的方法 B.控制变量法 C.等效替代法 D.类比法
(2)研究作用力一定时加速度与质量成反比的结论时,下列说法中正确的是D
A.平衡摩擦力时,应将装砂的小桶用细绳通过定滑轮系在小车上
B.每次改变小车质量时,要重新平衡摩擦力
C.实验时,先放开小车,再接通打点计时器的电源
D.在小车中增减砝码,应使小车和砝码的质量远大于砂和小桶的总质量
(3)某次实验中得到一条纸带,如图1所示,从比较清晰的点起,每5个计时点取一个计数点,分别标明0、l、2、3、4…,量得0与 1两点间距离x1=30mm,1与2两点间距离x2=36mm,2与3两点间距离x3=42mm,3与4两点间的距离x4=48mm,则小车在打计数点2时的瞬时速度为0.39 m/s,小车的加速度为0.6m/s2.

(4)某同学测得小车的加速度a和拉力F的数据如下表所示:(小车质量保持不变)
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/m•s-2 | 0.10 | 0.20 | 0.28 | 0.40 | 0.52 |
②图线不过原点的原因可能是没有平衡摩擦力或平衡摩擦力不够.
③图中的力F理论上指A,而实验中却用B表示.(选填字母符号)
A.绳对小车的拉力 B.砂和砂桶的重力.
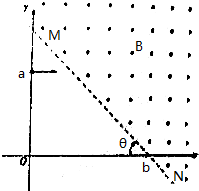 如图所示,纸面内有一直角坐标系xOy,a、b为坐标轴上的两点,其坐标分别为(0,2l)、(3l,0),直线MN过b点且可根据需要绕b点在纸面内转动,MN右侧存在垂直纸面向外的匀强磁场,磁感应强度大小为B,一质量为m,电荷量为q(q>0)的带电粒子从a点平行x轴射入第一象限,若MN绕b点转到合适位置,就能保证粒子经过磁场偏转后恰好能够到达b点,设MN与x轴负方向的夹角为θ,不计粒子重力.
如图所示,纸面内有一直角坐标系xOy,a、b为坐标轴上的两点,其坐标分别为(0,2l)、(3l,0),直线MN过b点且可根据需要绕b点在纸面内转动,MN右侧存在垂直纸面向外的匀强磁场,磁感应强度大小为B,一质量为m,电荷量为q(q>0)的带电粒子从a点平行x轴射入第一象限,若MN绕b点转到合适位置,就能保证粒子经过磁场偏转后恰好能够到达b点,设MN与x轴负方向的夹角为θ,不计粒子重力. 如图所,有一方向垂直纸面向里,宽度为L的匀强磁场,磁感应强度为B.有一等腰三角形导线框abc,ab为2L,线框总电阻为R;现让导线框以速度v匀速向右穿过磁场,规定a→b→c→a的电流方向为正方向,则线框穿过磁场过程中,电流随时间的变化规律图象正确的是 ( )
如图所,有一方向垂直纸面向里,宽度为L的匀强磁场,磁感应强度为B.有一等腰三角形导线框abc,ab为2L,线框总电阻为R;现让导线框以速度v匀速向右穿过磁场,规定a→b→c→a的电流方向为正方向,则线框穿过磁场过程中,电流随时间的变化规律图象正确的是 ( )



 如图所示,水平放置的平行板电容器与某一电源相连,它的极板长L=0.4m,两板间距离d=4×10-3 m,有一束由相同带电微粒组成的粒子流以相同的速度v0从两板中央平行极板射入,开关S闭合前,两极板间不带电,由于重力作用,微粒能落到下板的正中央.已知微粒质量m=4×10-5 kg,电荷量q=+1×10-8 C,g取10m/s2
如图所示,水平放置的平行板电容器与某一电源相连,它的极板长L=0.4m,两板间距离d=4×10-3 m,有一束由相同带电微粒组成的粒子流以相同的速度v0从两板中央平行极板射入,开关S闭合前,两极板间不带电,由于重力作用,微粒能落到下板的正中央.已知微粒质量m=4×10-5 kg,电荷量q=+1×10-8 C,g取10m/s2 如图所示,物体的质量为5kg,两根轻质细绳AB和AC的一端连接于竖直墙上的B、C两点,另一端系于物体上A点,(已知$\sqrt{6}$=2.449、$\sqrt{2}$=1.414、$\sqrt{3}$=1.732,g=10m/s2),求:
如图所示,物体的质量为5kg,两根轻质细绳AB和AC的一端连接于竖直墙上的B、C两点,另一端系于物体上A点,(已知$\sqrt{6}$=2.449、$\sqrt{2}$=1.414、$\sqrt{3}$=1.732,g=10m/s2),求: