题目内容
4.一个物体做自由落体运动,重力加速度g取1Om/s2.该物体( )| A. | 第2s末的速度大小为1Om/s | B. | 第2s末的速度大小为30m/s | ||
| C. | 在前3s内下落的距离为45m | D. | 在前3s内下落的距离为60m |
分析 自由落体的初速度为零,根据速度公式可求得物体下落的速度,根据位移公式可求得物体在3s内下落的高度.
解答 解:A、由速度公式可知,第2s末的速度大小为:v=gt=10×2=20m/s;故AB错误;
C、前3s内下落的距离为:h=$\frac{1}{2}g{t}^{2}$=$\frac{1}{2}×10×9$=45m;故C正确;D错误;
故选:C.
点评 本题考查自由落体规律的应用,要注意明确自由落体运动是初速度为零,加速度为g的匀加速直线运动.

练习册系列答案
相关题目
11.一卫星在赤道上空围绕地球做匀速圆周运动,飞行方向与地球的自转方向相同,轨道半径为r,转动周期大于地球自转周期T0=24h.已知地球半径为R,其表面的重力加速度为g,某时刻卫星通过赤道上某建筑物的上空,则到它下次通过该建筑物上空所需的时间为( )
| A. | $\frac{1}{\frac{1}{{T}_{0}}-\frac{1}{2π}\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B. | $\frac{1}{\frac{1}{{T}_{0}}+\frac{1}{2π}\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C. | 2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$ | D. | T0-2π$\sqrt{\frac{g{R}^{3}}{{r}^{3}}}$ |
19. 如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则(重力加速度为g)( )
如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则(重力加速度为g)( )
 如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则(重力加速度为g)( )
如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则(重力加速度为g)( )| A. | 可求M、N之间的距离 | |
| B. | 可求小球到达N点时的速度方向但不能求出大小 | |
| C. | 可求小球到达N点时的速度大小但不能求出方向 | |
| D. | 可以断定,当小球速度方向与斜面平行时,小球与斜面间的距离最大 |
9.一个质点做变速直线运动的v-t图象如图,下列说法中正确的是( )


| A. | 第1s内与第5s内的速度方向相反 | |
| B. | 第1s内的加速度大于第5s内的加速度 | |
| C. | 5秒末质点离出发点最远 | |
| D. | OA段的加速度与速度方向相同而BC段的加速度与速度方向相反 |
16.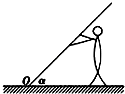 如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )
如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )
 如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )
如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )| A. | ω=$\frac{{v{{cos}^2}α}}{h}$ | B. | ω=$\frac{vsinα}{h}$ | C. | ω=$\frac{{v{{sin}^2}α}}{h}$ | D. | ω=$\frac{v}{hsinα}$ |
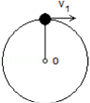 如图所示,质量m=0.1kg的小球在细绳的拉力作用下载竖直面内做半径为r=0.2m的圆周运动,g取10m/s2,求
如图所示,质量m=0.1kg的小球在细绳的拉力作用下载竖直面内做半径为r=0.2m的圆周运动,g取10m/s2,求
 (1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线方向保持水平;实验时,每次使小球由静止滚下都应注意从同一高度.
(1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线方向保持水平;实验时,每次使小球由静止滚下都应注意从同一高度.