题目内容
13. 如图所示,AOB是由某种透明物质制成的$\frac{1}{4}$圆柱体横截面(O为圆心),有一束平行单色光以45°的入射角射向柱体的OA平面,透明物质对该单色光的折射率为$\sqrt{2}$,这束光中有一部分不能从柱体的AB面上射出;设凡射到OB面的光全部被吸收,也不考虑OA面的反射.则圆柱体AB面上能射出光的部分占AB表面的( )
如图所示,AOB是由某种透明物质制成的$\frac{1}{4}$圆柱体横截面(O为圆心),有一束平行单色光以45°的入射角射向柱体的OA平面,透明物质对该单色光的折射率为$\sqrt{2}$,这束光中有一部分不能从柱体的AB面上射出;设凡射到OB面的光全部被吸收,也不考虑OA面的反射.则圆柱体AB面上能射出光的部分占AB表面的( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 画出光路图,当光线在AB弧面上发生全反射时,就没有光线从AB弧面射出,根据临界角确定出光线在AB弧面上恰好发生全反射时的入射点,由几何知识求解圆柱AB面上能射出光线的面积占AB表面积的几分之几.
解答  解:从O点射入的光线,折射角为r,根据折射定律有:
解:从O点射入的光线,折射角为r,根据折射定律有:
n=$\frac{sin45°}{sinr}$ ①
解得:
r=30° ②
从某位置P点入射的光线,折射到AB弧面上Q点时,入射角恰等于临界角C,有:
sinC=$\frac{1}{n}$ ③
代入数据得:
C=45° ④
△PQO中∠α=180°-90°-C-r=15°
所以能射出的光线区域对应的圆心角:
β=90°-α-r=45°⑥
能射出光线的部分占AB面的比例为:
$\frac{45°}{90°}$=$\frac{1}{2}$ ⑦
故选:C
点评 正确地画出光路图是解决本题问题的关键,是折射定律和几何知识的结合应用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.下列说法正确的有( )
| A. | 经典物理学适用于宏观低速领域,具有局限性 | |
| B. | 光具有波动性和粒子性,即波粒二象性 | |
| C. | 电动机利用了通电线圈在磁场中受到的安培力的作用原理 | |
| D. | 利用科技手段可以使物体的速度达到3.5×108m/s | |
| E. | 手机通信必须依靠电磁波 | |
| F. | 红外线人体测温仪可以迅速测量体温,它是一种传感器 | |
| G. | 只要把闭合线圈放在磁感应强度很大匀强磁场中,并且让磁感线穿过线圈,线圈一定会产生感应电流 | |
| H. | 闭合线圈如果在磁场中作切割磁感线的运动,一定会产生感应电流 |
18.快热式电热水器,也叫即热电热水器,它无需巨大的储水桶,不需预热和保温.通电通水后打开出水口几秒种就会流出热水,即开、即热、即用、即停,省时、省电、省水、省空间,因此有逐渐替代储水式电热水器的趋势.如表是某快热式电热水器的铭牌,求该电热水器正常工作时:
(1)通过电热水器的电流;
(2)电热水器工作100s产生的热量.
| 快热式电热水器 | |
| 型号 | DSF-S6-80 |
| 额定电压 | 220V~ |
| 额定频率 | 50Hz |
| 额定功率 | 8800W |
| 额定压力 | 0.6Mpa |
| 防水等级 | LPX 4 |
(2)电热水器工作100s产生的热量.
2.LC回路中电容器两端电压U随时间t变化的关系如图所示,则( )
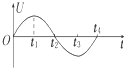

| A. | 在时刻t2,电路中的电流为零 | |
| B. | 在时刻t3,电路中的磁场能最大 | |
| C. | 从时刻t2至t3,电路中的电场能不断增大 | |
| D. | 从时刻t3至t4,电容器所带的电荷量不断增大 |
3.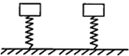 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )| A. | 两物块达最大速度时的高度相同 | B. | 上升的最大高度不同 | ||
| C. | 最大加速度相同 | D. | 最大重力势能不同 |




 如图所示,一小锤用细线系于固定悬挂点O处,将小锤拉至O左侧一定高度(不超过O点所在的水平面)由静止释放,小锤恰好在最低点P与停在光滑水平面上的物块发生弹性正碰,碰后物块冲向右边固定在墙上的细长钢钉.已知物块和小锤的质量分别为m、3m;物块和钢钉的长度分别为l、2l,OP距离为R;当小锤释放点距离P的高度h=$\frac{R}{2}$时,物块最终停止时其右端到墙的水平距离为$\frac{l}{2}$.重力加速度为g.物块未被穿透时受到的阻力大小只与钢钉进入物块的深度有关,物块被穿透后受到的阻力恒为f0.
如图所示,一小锤用细线系于固定悬挂点O处,将小锤拉至O左侧一定高度(不超过O点所在的水平面)由静止释放,小锤恰好在最低点P与停在光滑水平面上的物块发生弹性正碰,碰后物块冲向右边固定在墙上的细长钢钉.已知物块和小锤的质量分别为m、3m;物块和钢钉的长度分别为l、2l,OP距离为R;当小锤释放点距离P的高度h=$\frac{R}{2}$时,物块最终停止时其右端到墙的水平距离为$\frac{l}{2}$.重力加速度为g.物块未被穿透时受到的阻力大小只与钢钉进入物块的深度有关,物块被穿透后受到的阻力恒为f0. 如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.