��Ŀ����
3��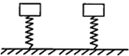 ��ͼ��ʾ��������ȫ��ͬ�����ʵ��ɣ��¶˹̶��ڵ����ϣ�������ͬ����״��ͬ�������ֱ������������϶˵���˨�ӣ��������������������ϣ�ʹ�����ɾ�����ͬ��ѹ��������ȥ������������ɾ�ֹ�����˶����뿪���ɣ���ӳ�ȥ����������ٶȵ�һ�μ�Ϊ��Ĺ��̣������һ�����㣨����ʼ���ڵ�����֮�ڣ��Ե���Ϊ�������棩��������
��ͼ��ʾ��������ȫ��ͬ�����ʵ��ɣ��¶˹̶��ڵ����ϣ�������ͬ����״��ͬ�������ֱ������������϶˵���˨�ӣ��������������������ϣ�ʹ�����ɾ�����ͬ��ѹ��������ȥ������������ɾ�ֹ�����˶����뿪���ɣ���ӳ�ȥ����������ٶȵ�һ�μ�Ϊ��Ĺ��̣������һ�����㣨����ʼ���ڵ�����֮�ڣ��Ե���Ϊ�������棩��������| A�� | ����������ٶ�ʱ�ĸ߶���ͬ | B�� | ���������߶Ȳ�ͬ | ||
| C�� | �����ٶ���ͬ | D�� | ����������ܲ�ͬ |
���� �ٶ����ʱ�����뵯�ɵĵ���ƽ�⣬��ʽ������ʱ�߶ȵĹ�ϵ��������ѹ������ͬ��������ӵĵ���������ͬ���ɻ�е���غ㶨�ɿ���ȷ�������ܼ����ܵĹ�ϵ��ע�����������������ͬ��Ӱ�죮
��� �⣺A���ٶ����ʱ���� kx=mg���ɵ�ѹ���� x=$\frac{mg}{k}$��k��ͬ��m��ͬ����x��ͬ����������ٶ�ʱ�ĸ߶Ȳ�ͬ����A����
BD�����ڿ�ʼʱ���ɵ�ѹ������ͬ���ɵĵ���������ͬ��������뵯��ϵͳ�Ļ�е���غ㶨�ɿ�֪���������ܵ�������һ�����ڵ������ܣ����������ܵı仯����ͬ��ԭ�����������ܲ�ͬ��������������ܲ�ͬ�������������������ͬ�������������߶Ȳ�ͬ����B��ȷ��D��ȷ��
C���ճ�ȥ����ʱ���ٶ������a=$\frac{F}{m}$��֪ԭ�����ɵĵ�����ͬ������F��ͬ���������������ͬ���������ٶȲ�ͬ����C����
��ѡ��BD��
���� ���⿼���е���غ㶨�ɼ�ţ�ٵڶ����ɣ�Ҫע����ȷ��ȷ���ɵĵ�������ȡ���ڵ��ɵ��α���������ϵ����

��ϰ��ϵ�д�
�����Ŀ
13�� ��ͼ��ʾ��AOB����ij���������Ƴɵ�$\frac{1}{4}$Բ�������棨OΪԲ�ģ�����һ��ƽ�е�ɫ����45�����������������OAƽ�棬�����ʶԸõ�ɫ���������Ϊ$\sqrt{2}$������������һ���ֲ��ܴ������AB����������跲�䵽OB��Ĺ�ȫ�������գ�Ҳ������OA��ķ��䣮��Բ����AB�����������IJ���ռAB����ģ�������
��ͼ��ʾ��AOB����ij���������Ƴɵ�$\frac{1}{4}$Բ�������棨OΪԲ�ģ�����һ��ƽ�е�ɫ����45�����������������OAƽ�棬�����ʶԸõ�ɫ���������Ϊ$\sqrt{2}$������������һ���ֲ��ܴ������AB����������跲�䵽OB��Ĺ�ȫ�������գ�Ҳ������OA��ķ��䣮��Բ����AB�����������IJ���ռAB����ģ�������
 ��ͼ��ʾ��AOB����ij���������Ƴɵ�$\frac{1}{4}$Բ�������棨OΪԲ�ģ�����һ��ƽ�е�ɫ����45�����������������OAƽ�棬�����ʶԸõ�ɫ���������Ϊ$\sqrt{2}$������������һ���ֲ��ܴ������AB����������跲�䵽OB��Ĺ�ȫ�������գ�Ҳ������OA��ķ��䣮��Բ����AB�����������IJ���ռAB����ģ�������
��ͼ��ʾ��AOB����ij���������Ƴɵ�$\frac{1}{4}$Բ�������棨OΪԲ�ģ�����һ��ƽ�е�ɫ����45�����������������OAƽ�棬�����ʶԸõ�ɫ���������Ϊ$\sqrt{2}$������������һ���ֲ��ܴ������AB����������跲�䵽OB��Ĺ�ȫ�������գ�Ҳ������OA��ķ��䣮��Բ����AB�����������IJ���ռAB����ģ�������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
11�� ��ͼ��ʾ��������������϶���������ת��A���ӣ�����¶˹̶�һ����Ȼ�쳤�������ᵯ�ɣ�Χ�ɱ߳�ΪL�ĵȱ�������ABC������װ����ֱ���ڹ⻬ˮƽ���ϣ�����A��ʩ����ֱ���µĴ�СΪF�������������ɱ�����һ�����ȣ�����ʱ���ɵ�����СǡΪ$\frac{F}{2}$���ɵľ���ϵ��Ϊ��������
��ͼ��ʾ��������������϶���������ת��A���ӣ�����¶˹̶�һ����Ȼ�쳤�������ᵯ�ɣ�Χ�ɱ߳�ΪL�ĵȱ�������ABC������װ����ֱ���ڹ⻬ˮƽ���ϣ�����A��ʩ����ֱ���µĴ�СΪF�������������ɱ�����һ�����ȣ�����ʱ���ɵ�����СǡΪ$\frac{F}{2}$���ɵľ���ϵ��Ϊ��������
 ��ͼ��ʾ��������������϶���������ת��A���ӣ�����¶˹̶�һ����Ȼ�쳤�������ᵯ�ɣ�Χ�ɱ߳�ΪL�ĵȱ�������ABC������װ����ֱ���ڹ⻬ˮƽ���ϣ�����A��ʩ����ֱ���µĴ�СΪF�������������ɱ�����һ�����ȣ�����ʱ���ɵ�����СǡΪ$\frac{F}{2}$���ɵľ���ϵ��Ϊ��������
��ͼ��ʾ��������������϶���������ת��A���ӣ�����¶˹̶�һ����Ȼ�쳤�������ᵯ�ɣ�Χ�ɱ߳�ΪL�ĵȱ�������ABC������װ����ֱ���ڹ⻬ˮƽ���ϣ�����A��ʩ����ֱ���µĴ�СΪF�������������ɱ�����һ�����ȣ�����ʱ���ɵ�����СǡΪ$\frac{F}{2}$���ɵľ���ϵ��Ϊ��������| A�� | $\frac{F}{��\sqrt{2}-1��L}$ | B�� | $\frac{F}{2��\sqrt{2}-1��L}$ | C�� | $\frac{F}{��\sqrt{5}-1��L}$ | D�� | $\frac{F}{2��\sqrt{5}-1��L}$ |
18��һ�м�г�Შ��x������������x=2m�����ʵ����ͼ����ͼ1��ʾ����x=8m�����ʵ����ͼ����ͼ2��ʾ������˵����ȷ���ǣ�������


| A�� | �ò�������Ϊ12s | |
| B�� | x=2m�����ʵ���ƽ��λ����+y������ʱ��x=8m�����ʵ��ڲ��� | |
| C�� | ��0��4s��x=2m����x=8m�����ʵ�ͨ����·�̾�Ϊ6cm | |
| D�� | �ò��IJ�������Ϊ8m | |
| E�� | �ò��Ĵ����ٶȿ���Ϊ2m/s |

 ��ͼ��ʾ���⻬��Ե��ˮƽ������ˮƽ���ҵ���ǿ�糡���糡ǿ��E=2.0��104N/C�����ף������硢�ɿ����ʵ㣩�����������´�A����a1=10m/s2�ļ��ٶ��ɾ�ֹ��ʼ�������ȼ����˶���ͬʱ����m=1.0��10-1kg��������Ϊq=+2.0��10-5C������Ҵ�B���Գ��ٶ�v0�����ȼ����˶������˶���C��ʱȥ���������ã��ס��ҿ�ʼ�˶�ʱ��ʼ��ʱ��t=1.0sʱ���������������֪A��C�����ľ���s1=0.2m��B��C�����ľ���s2=4.0m���������ٶ�g=10m/s2����
��ͼ��ʾ���⻬��Ե��ˮƽ������ˮƽ���ҵ���ǿ�糡���糡ǿ��E=2.0��104N/C�����ף������硢�ɿ����ʵ㣩�����������´�A����a1=10m/s2�ļ��ٶ��ɾ�ֹ��ʼ�������ȼ����˶���ͬʱ����m=1.0��10-1kg��������Ϊq=+2.0��10-5C������Ҵ�B���Գ��ٶ�v0�����ȼ����˶������˶���C��ʱȥ���������ã��ס��ҿ�ʼ�˶�ʱ��ʼ��ʱ��t=1.0sʱ���������������֪A��C�����ľ���s1=0.2m��B��C�����ľ���s2=4.0m���������ٶ�g=10m/s2���� ��ͼ��ʾ��Ϊһ��Լ��װ�õ�ԭ��ͼ��Բ��Ϊԭ��O���뾶ΪR0��Բ����������з���ֱxoyƽ���������ǿ�ų���һ������Ϊm������Ϊq���������Ӵ�����Ϊ��0��R0����A����y�Ḻ�������ٶ�v0����ų����������ȫ������x���ϵ�P�㣬������x���������ڻ����������Ϸ���ֱ��xoyƽ�����ǿ�ų�ʱ�����������Դ�A����y�Ḻ����������������Ӿ����������Q���2�������������֪OQ��x���������600���������������Ӽ������ã���
��ͼ��ʾ��Ϊһ��Լ��װ�õ�ԭ��ͼ��Բ��Ϊԭ��O���뾶ΪR0��Բ����������з���ֱxoyƽ���������ǿ�ų���һ������Ϊm������Ϊq���������Ӵ�����Ϊ��0��R0����A����y�Ḻ�������ٶ�v0����ų����������ȫ������x���ϵ�P�㣬������x���������ڻ����������Ϸ���ֱ��xoyƽ�����ǿ�ų�ʱ�����������Դ�A����y�Ḻ����������������Ӿ����������Q���2�������������֪OQ��x���������600���������������Ӽ������ã��� ��ͼ��ʾ���̶���ˮƽ�����ϵĹ⻬��ֱ����ۣ���ͼΪ����ͼ��ͼ������ƽ��˫ֱ�߱�ʾ�۵�����ڣ������ڷ���һ�����飬�������벿�ǰ뾶ΪR�İ�Բ���ι⻬���ۣ�����Ŀ���Ϊ2R��ǡ��۵����ڲ�ڵļ����ȣ�������ڲ����ز۱����ɻ���������һ����С����Ϊ�ʵ㣩��ˮƽ���ٶ�v0�ز۵�һ��ڳ��飬�ӻ���İ�Բ�βۿڱ�Ե���뻬�鰼�ۣ���֪����С�������Ϊm�����������Ϊ3m�������˶���������е����ʧ����
��ͼ��ʾ���̶���ˮƽ�����ϵĹ⻬��ֱ����ۣ���ͼΪ����ͼ��ͼ������ƽ��˫ֱ�߱�ʾ�۵�����ڣ������ڷ���һ�����飬�������벿�ǰ뾶ΪR�İ�Բ���ι⻬���ۣ�����Ŀ���Ϊ2R��ǡ��۵����ڲ�ڵļ����ȣ�������ڲ����ز۱����ɻ���������һ����С����Ϊ�ʵ㣩��ˮƽ���ٶ�v0�ز۵�һ��ڳ��飬�ӻ���İ�Բ�βۿڱ�Ե���뻬�鰼�ۣ���֪����С�������Ϊm�����������Ϊ3m�������˶���������е����ʧ���� �����ʹ���������ͬ���������ӣ��Բ�ͬ�����ʴ�ֱ�ڴŸ��߷���������ǿ�ų��У������ӵ��˶��켣��ͼ�Т١�����ʾ�����ӵ��������ƣ����ж��������ӵ��˶����ʦԺ��ڴų����˶�ʱ��t���˶�����T�����ٶȵ�˵������ȷ���ǣ�������
�����ʹ���������ͬ���������ӣ��Բ�ͬ�����ʴ�ֱ�ڴŸ��߷���������ǿ�ų��У������ӵ��˶��켣��ͼ�Т١�����ʾ�����ӵ��������ƣ����ж��������ӵ��˶����ʦԺ��ڴų����˶�ʱ��t���˶�����T�����ٶȵ�˵������ȷ���ǣ�������