题目内容
 如图所示,固定的竖直大圆环半径为R,劲度系数为k的弹簧原长为L(L<2R),其上端悬挂于大圆环最高点A,下端连接一重为G的光滑小滑环P,小滑环套在大圆环上,当小滑环P静止时,弹簧与竖直方向的夹角为多少?
如图所示,固定的竖直大圆环半径为R,劲度系数为k的弹簧原长为L(L<2R),其上端悬挂于大圆环最高点A,下端连接一重为G的光滑小滑环P,小滑环套在大圆环上,当小滑环P静止时,弹簧与竖直方向的夹角为多少?
解:以小环为研究对象,分析受力情况,如图.

根据平衡条件得知,大圆环对小环的压力N和弹簧的弹力F的合力与力大小相等,方向相反,G′=G,根据△G′NP∽△APO得:
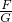 =
=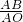
又AP=2Rcosθ,AO=R,弹簧的弹力为:F=k(2Rcosθ-L)
代入得:
 =
=
解得:θ=arccos
答:当小滑环P静止时,弹簧与竖直方向的夹角为arccos .
.
分析:以小球为研究对象,分析受力情况,作出力图.根据平衡条件,运用三角形相似法得到弹簧的弹力大小,再由胡克定律和几何知识求出弹簧与竖直方向的夹角θ.
点评:本题涉及非直角三角形的力平衡问题,运用三角相似法处理,也可以运用三角函数法研究.

根据平衡条件得知,大圆环对小环的压力N和弹簧的弹力F的合力与力大小相等,方向相反,G′=G,根据△G′NP∽△APO得:
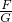 =
=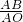
又AP=2Rcosθ,AO=R,弹簧的弹力为:F=k(2Rcosθ-L)
代入得:
 =
=
解得:θ=arccos

答:当小滑环P静止时,弹簧与竖直方向的夹角为arccos
 .
.分析:以小球为研究对象,分析受力情况,作出力图.根据平衡条件,运用三角形相似法得到弹簧的弹力大小,再由胡克定律和几何知识求出弹簧与竖直方向的夹角θ.
点评:本题涉及非直角三角形的力平衡问题,运用三角相似法处理,也可以运用三角函数法研究.

练习册系列答案
相关题目
 如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,粗筒中A、B两轻质光滑活塞间封有理想气体,活塞A上方有水银.水银深H=10cm,气柱长L=20cm,大气压强p0=75cm Hg.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,现保持温度不变,使活塞B缓慢上移,直到水银的一半被推入细筒,这个过程中,下列说法正确的是( )
如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,粗筒中A、B两轻质光滑活塞间封有理想气体,活塞A上方有水银.水银深H=10cm,气柱长L=20cm,大气压强p0=75cm Hg.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,现保持温度不变,使活塞B缓慢上移,直到水银的一半被推入细筒,这个过程中,下列说法正确的是( )| A、筒内气体的压强逐渐变大,最后变为100cmHg | B、气体向外放出热量 | C、单位时间碰撞到活塞上的气体分子个数减少 | D、活塞B向上移动的距离为17cm |
 如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,水银深H=10cm,气柱长L=20cm,大气压强p0=75cmHg.现使活塞B缓慢上移,直到水银的一半被推入细筒中,则此时筒内气体的压强为
如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,水银深H=10cm,气柱长L=20cm,大气压强p0=75cmHg.现使活塞B缓慢上移,直到水银的一半被推入细筒中,则此时筒内气体的压强为 如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞导热性能良好,其间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,水银深H=10cm,气柱长L=20cm,大气压强p0=75cmHg.现使活塞B缓慢上移,直到A活塞上移H/2的距离,气体温度不变.则对于被封气体:
如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞导热性能良好,其间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,水银深H=10cm,气柱长L=20cm,大气压强p0=75cmHg.现使活塞B缓慢上移,直到A活塞上移H/2的距离,气体温度不变.则对于被封气体: 如图所示,固定的竖直大圆环半径为R,劲度系数为k的弹簧原长为L(L<2R),其上端悬挂于大圆环最高点A,下端连接一重为G的光滑小滑环P,小滑环套在大圆环上,当小滑环P静止时,弹簧与竖直方向的夹角为多少?
如图所示,固定的竖直大圆环半径为R,劲度系数为k的弹簧原长为L(L<2R),其上端悬挂于大圆环最高点A,下端连接一重为G的光滑小滑环P,小滑环套在大圆环上,当小滑环P静止时,弹簧与竖直方向的夹角为多少?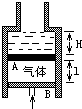 (2011?崇明县二模)如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,当时气体温度为23℃水银深H=10cm,气柱长L=20cm,大气压强p0=75cm Hg.现保持温度不变,使活塞B缓慢上移,直到水银的一半被推入细筒中,
(2011?崇明县二模)如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,当时气体温度为23℃水银深H=10cm,气柱长L=20cm,大气压强p0=75cm Hg.现保持温度不变,使活塞B缓慢上移,直到水银的一半被推入细筒中,