题目内容
1. 电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d有平行边界的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度(已知电子的质量为m,电荷量为e).
电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d有平行边界的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度(已知电子的质量为m,电荷量为e).
分析 根据动能定理求出电子经电场加速后的速度,根据几何关系求出粒子在磁场中的半径,结合半径公式求出磁感应强度的大小.
解答 解:电子经电场加速后,根据动能定理有:$eU=\frac{1}{2}m{v^2}$ …①
…①
电子进入磁场后,洛伦兹力充当向心力:$eBv=m\frac{v^2}{r}$…②
由几何关系得:r2=d2+(r-L)2…③
由①②③解得:B=$\frac{{2L\sqrt{\frac{2mU}{e}}}}{{{d^2}+{L^2}}}$.
答:匀强磁场的磁感应强度为$\frac{{2L\sqrt{\frac{2mU}{e}}}}{{{d^2}+{L^2}}}$.
点评 本题是带电粒子在磁场中运动的问题,关键是画出轨迹,由几何知识求解轨迹半径.

练习册系列答案
相关题目
12.如图为探究产生电磁感应现象条件的实验装置,下列情况中能引起电流计指针转动的是( )


| A. | 闭合电键以后一直保持闭合状态 | |
| B. | 闭合电键以后,再断开电键瞬间 | |
| C. | 断开电键以后拿出线圈A中铁芯瞬间 | |
| D. | 断开电键使变阻器的滑动头向右移动 |
10.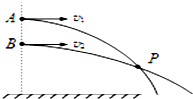 如图所示,从同一竖直线上不同高度A、B两点处,分别以速率v1、v2同向水平抛出两个小球,P为它们运动轨迹的交点.则下列说法正确的有( )
如图所示,从同一竖直线上不同高度A、B两点处,分别以速率v1、v2同向水平抛出两个小球,P为它们运动轨迹的交点.则下列说法正确的有( )
 如图所示,从同一竖直线上不同高度A、B两点处,分别以速率v1、v2同向水平抛出两个小球,P为它们运动轨迹的交点.则下列说法正确的有( )
如图所示,从同一竖直线上不同高度A、B两点处,分别以速率v1、v2同向水平抛出两个小球,P为它们运动轨迹的交点.则下列说法正确的有( )| A. | 两球在P点一定具有相同的速率 | |
| B. | 若同时抛出,两球不可能在P点相碰 | |
| C. | 若同时抛出,落地前两球竖直方向的距离逐渐变大 | |
| D. | 若同时抛出,落地前两球之间的距离逐渐变大 |
 如图所示的空间有一竖直向下的匀强电场,场强E=2×103N/C,有一个可视为质点的质量为m=1kg,电荷量q=+1×10-3C的小物块,从光滑平台上的A点以v0=2m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=3kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R=0.4m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,g取10m/s2.求:
如图所示的空间有一竖直向下的匀强电场,场强E=2×103N/C,有一个可视为质点的质量为m=1kg,电荷量q=+1×10-3C的小物块,从光滑平台上的A点以v0=2m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=3kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R=0.4m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,g取10m/s2.求:
 如图,物体从高H为7.8m的A处,以某一初速度V0沿光滑曲面滑至B点,然后再沿水平面运动,通过40m距离到达C点时的速度为4m/s,物体与水平面间的滑动摩擦系数μ=0.3,求:
如图,物体从高H为7.8m的A处,以某一初速度V0沿光滑曲面滑至B点,然后再沿水平面运动,通过40m距离到达C点时的速度为4m/s,物体与水平面间的滑动摩擦系数μ=0.3,求: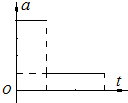 一滑块以一定的初速度从一固定斜面的底端向上冲,到斜面上某一点后返回底端,斜面粗糙.滑块运动过程中加速度与时间关系图象如图所示.下列四幅图象分别表示滑块运动过程中位移x、速度v、动能Ek和重力势能Ep(以斜面底端为参考平面)随时间变化的关系图象,其中正确的是( )
一滑块以一定的初速度从一固定斜面的底端向上冲,到斜面上某一点后返回底端,斜面粗糙.滑块运动过程中加速度与时间关系图象如图所示.下列四幅图象分别表示滑块运动过程中位移x、速度v、动能Ek和重力势能Ep(以斜面底端为参考平面)随时间变化的关系图象,其中正确的是( )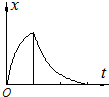
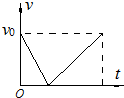

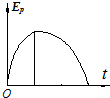
 如图所示,U形管右管横截面积为左管横截面积的2倍,在左管内用水银封闭一段长为30cm、温度为577.5K的空气柱,左右两管水银面高度差为21cm,外界大气压为76cmHg.若给左管的封闭气体降温,使管内气柱长度变为20cm.求:
如图所示,U形管右管横截面积为左管横截面积的2倍,在左管内用水银封闭一段长为30cm、温度为577.5K的空气柱,左右两管水银面高度差为21cm,外界大气压为76cmHg.若给左管的封闭气体降温,使管内气柱长度变为20cm.求: