题目内容
16．
如图所示，一足够长的绝缘材料的光滑斜面与地面成θ角，其上端放有一块质量为m，带有负电荷q的金属块，整个装置放在垂直于纸面向外的匀强磁场中，其磁感应强度为B，求：（1）金属块开始下滑时的加速度a
（2）它沿斜面的最大速度．
分析 金属块受重力、支持力、洛伦兹力，平行斜面方向做匀加速直线运动，垂直斜面方向受力平衡，当洛伦兹力增加到等于重力的垂直分力时，金属块开始离开斜面．
解答 解：（1）以金属块为研究对象，分析其受力情况：受重力、斜面支持力及洛伦兹力作用，沿斜面方向上；
根据牛顿第二定律，有：mgsinθ=ma；
在垂直于斜面方向上，有：FN+Ff洛=mgcosθ；
故开始时刻的加速度为：a=gsinθ；
（2）由Ff洛=qυB，知Ff洛随着金属块运动速度的增大而增大．
当Ff洛增大到使FN=0时，金属块将脱离斜面，此时Ff洛=qυmB=mgcosθ．
所以：υm=$\frac{mgcosθ}{qB}$，此即为金属块在斜面上运动速度的最大值．
答：（1）金属块开始下滑时的速度a为gsinθ；
（2）它沿斜面的最大速度为$\frac{mgcosθ}{qB}$．
点评 本题关键明确金属块的受力情况，根据牛顿第二定律求解出加速度后运用运动学公式和平衡条件求解出沿斜面过程的最大速度．
练习册系列答案
相关题目
如图所示，将打点计时器固定在铁架台上，让重物带动纸带从静止开始自由下落，利用此装置可测定重力加速度．
7．
如图所示，一列横波在t1和t2两时刻的波形分别如图中的实线和虚线所示，已知波在介质中的传播速度是2m/s．下述结论正确的是（ ）
如图所示，一列横波在t1和t2两时刻的波形分别如图中的实线和虚线所示，已知波在介质中的传播速度是2m/s．下述结论正确的是（ ）| A． | 若t2-t1=1.5s，则此过程中质点Q沿传播方向移动3m | |
| B． | 若t2-t1=1.5s，则波是向左传播的 | |
| C． | 若t2-t1=2.5s，则t2时刻质点Q的加速度向上 | |
| D． | 若t2-t1=2.5s，则在t1时刻质点P向上运动 |
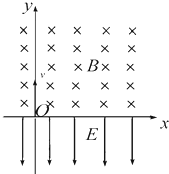如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E．一质量为m，电量为-q的粒子从坐标原点O沿着y轴正方向射出?射出之后，第三次到达x轴时（O点不算第一次），它与点O的距离为L．求：
要精确测量一个阻值约为5Ω的电阻R，实验提供下列器材：
如图所示，质量为m的物块A被轻质细绳系住斜吊着放在倾角为30°的静止斜面上，物块A与斜面间的动摩擦因数μ（μ＜$\frac{\sqrt{3}}{3}$），细绳绕过定滑轮O，左右两边与竖直方向的夹角α=30°、β=60°，细绳右端固定在天花板上，O′为细绳上一光滑动滑轮，下方悬挂着重物B．整个装置处于静止状态，重力加速度为g，最大静摩擦力近似等于滑动摩擦力，不考虑动滑轮重力，求：
在地面上有竖直放置的静止物体A和B，A、B之间用不计质量的轻弹簧栓接在一起，弹簧的劲度系数k=100N/m，A、B的质量都为1kg，现用F=20N的竖直向上恒力作用在物体A上，使A竖直上升，重力加速度g=10m/s2，设弹簧始终是在弹性限度内，空气阻力不计．求
如图所示，正方形匀强磁场的边界长为a，边界由绝缘弹性壁围成，磁场的磁感应强度为B，质量为m、电荷量为q的带正电粒子垂直于磁场方向和边界从边界正中点O处射入磁场，其射入时的速度为$\frac{17Bqa}{8m}$，带电粒子与壁碰撞前后沿壁方向的分速度不变，垂直壁方向的分速度反向、大小不变，且不计摩擦，不计粒子所受重力，碰撞时无电荷量损失，求：
如图所示，在倾角为θ的斜面上，固定一宽度为L的平行金属导轨，在导轨上端接入电源和滑动变阻器R．电源电动势为E，内阻为r，一质量为m的金属棒ab与两导轨垂直并接触良好．整个装置处于磁感应强度为B、垂直于斜面向上的匀强磁场中（导轨与金属棒的电阻不计）．金属导轨是光滑的，要保持金属棒在导轨上静止，求：