题目内容
10. 质量为m的带电小球用不可伸长的绝缘线悬挂于O点,并处在水平向右的大小为E的边界足够大的匀强电场中,小球静止时丝线与竖直方向的夹角为θ,如图所示,问:
质量为m的带电小球用不可伸长的绝缘线悬挂于O点,并处在水平向右的大小为E的边界足够大的匀强电场中,小球静止时丝线与竖直方向的夹角为θ,如图所示,问:(1)小球带正电还是负电?所带电荷量是多少?
(2)丝线烧断后经过时间t,小球的动能多大?
(3)剪断细线1s,小球发生的位移是多少?
分析 (1)小球向右偏,做带正电,可由受力平衡算出其电量;
(2)把悬线烧断后小球受两个恒力作用,故作匀加速直线运动,求的加速度,由vat求的速度,即可求得动能
(3)小球做初速度为零的运动加速运动,由运动学公式即可求得
解答 解:(1)小球带正电
分析如图,根据平衡条件得Eq=mgtanθ
q=$\frac{mgtanθ}{E}$
(2)小球得加速度为a=$\frac{\sqrt{(qE)^{2}+(mg)^{2}}}{m}=\frac{g}{cosθ}$
ts时的速度为v=at=$\frac{gt}{cosθ}$
动能为${E}_{k}=\frac{1}{2}m{v}^{2}=\frac{m{g}^{2}{t}^{2}}{2co{s}^{2}θ}$
(3)剪短后小球做匀加速运动,故通过的位移为$x=\frac{1}{2}a{t}^{2}=\frac{g}{2cosθ}$
答:(1)小球带正电,所带电荷量是$\frac{mgtanθ}{E}$
(2)丝线烧断后经过时间t,小球的动能为$\frac{m{g}^{2}{t}^{2}}{2co{s}^{2}θ}$
(3)剪断细线1s,小球发生的位移是$\frac{g}{2cosθ}$
点评 对于带电体在电场力平衡问题,关键是分析受力情况,运用力学方法求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.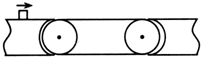 水平传送装置如图所示,一物块每次都以恒定的初速度由载物台冲上传送带,当传送带顺时针方向转动时,通过传送带所用时间为t1;当传送带逆时针方向转动时,通过传送带所用时间为t2;当传送带不动时,通过传送带所用时间为t3.下列判断正确的是( )
水平传送装置如图所示,一物块每次都以恒定的初速度由载物台冲上传送带,当传送带顺时针方向转动时,通过传送带所用时间为t1;当传送带逆时针方向转动时,通过传送带所用时间为t2;当传送带不动时,通过传送带所用时间为t3.下列判断正确的是( )
 水平传送装置如图所示,一物块每次都以恒定的初速度由载物台冲上传送带,当传送带顺时针方向转动时,通过传送带所用时间为t1;当传送带逆时针方向转动时,通过传送带所用时间为t2;当传送带不动时,通过传送带所用时间为t3.下列判断正确的是( )
水平传送装置如图所示,一物块每次都以恒定的初速度由载物台冲上传送带,当传送带顺时针方向转动时,通过传送带所用时间为t1;当传送带逆时针方向转动时,通过传送带所用时间为t2;当传送带不动时,通过传送带所用时间为t3.下列判断正确的是( )| A. | 一定有t1<t2 | B. | 一定有t2>t3>t1 | C. | 可能有t1=t2=t3 | D. | 可能有t1<t2=t3 |
2.传感器的种类多种多样,其性能也各不相同,空调机在室内温度达到设定的温度后,会自动停止工作,空调机内使用的传感器是( )
| A. | 生物传感器 | B. | 红外传感器 | C. | 温度传感器 | D. | 压力传感器 |
19.一观察者发现,每隔一定时间有一滴水自8m高的屋檐自由落下,而且当看到第五滴水刚要离开屋檐时,第一滴水正好落到地面,那么,这时第二滴水离地的高度是( )
| A. | 3.5m | B. | 2.9m | C. | 2.5m | D. | 2m |
20. 如图所示,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{5π}$T,单匝矩形线圈面积S=1m2,电阻不计,绕垂直于磁场的轴OO′匀速转动.线圈通过电刷与一理想变压器原线圈相接,
如图所示,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{5π}$T,单匝矩形线圈面积S=1m2,电阻不计,绕垂直于磁场的轴OO′匀速转动.线圈通过电刷与一理想变压器原线圈相接, 为交流电流表.调整副线圈的滑动触头P,当变压器原、副线圈匝数比为1:2时,副线圈电路中标有“36V 36W”的灯泡正常发光.以下判断正确的是( )
为交流电流表.调整副线圈的滑动触头P,当变压器原、副线圈匝数比为1:2时,副线圈电路中标有“36V 36W”的灯泡正常发光.以下判断正确的是( )
 如图所示,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{5π}$T,单匝矩形线圈面积S=1m2,电阻不计,绕垂直于磁场的轴OO′匀速转动.线圈通过电刷与一理想变压器原线圈相接,
如图所示,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{5π}$T,单匝矩形线圈面积S=1m2,电阻不计,绕垂直于磁场的轴OO′匀速转动.线圈通过电刷与一理想变压器原线圈相接, 为交流电流表.调整副线圈的滑动触头P,当变压器原、副线圈匝数比为1:2时,副线圈电路中标有“36V 36W”的灯泡正常发光.以下判断正确的是( )
为交流电流表.调整副线圈的滑动触头P,当变压器原、副线圈匝数比为1:2时,副线圈电路中标有“36V 36W”的灯泡正常发光.以下判断正确的是( )| A. | 电流表的示数为1A | |
| B. | 矩形线圈产生电动势的有效值为18$\sqrt{2}$V | |
| C. | 从矩形线圈转到中性面开始计时,线圈电动势随时间的变化规律e=18$\sqrt{2}$sin90πt(V) | |
| D. | 若矩形线圈转速减小,为使灯泡仍能正常发光,应将P适当上移 |
 如图所示,足够长光滑水平轨道与半径为R的光滑四分之一圆弧轨道相切.现从圆弧轨道的最高点由静止释放一质量为m的弹性小球A,当A球刚好运动到圆弧轨道的最低点时,与静止在该点的另一弹性小球B发生弹性碰撞.已知B球的质量是A球质量的k倍,且两球均可看成质点.
如图所示,足够长光滑水平轨道与半径为R的光滑四分之一圆弧轨道相切.现从圆弧轨道的最高点由静止释放一质量为m的弹性小球A,当A球刚好运动到圆弧轨道的最低点时,与静止在该点的另一弹性小球B发生弹性碰撞.已知B球的质量是A球质量的k倍,且两球均可看成质点. 图中水平桌面上的滑块质量为M,一条绳其两端分别系着质量为m1,m2的两个物体的不计质量,不可伸长的细绳套在滑块上,滑块、绳子与桌面相互间均无摩擦,求运动过程中滑块的加速度.
图中水平桌面上的滑块质量为M,一条绳其两端分别系着质量为m1,m2的两个物体的不计质量,不可伸长的细绳套在滑块上,滑块、绳子与桌面相互间均无摩擦,求运动过程中滑块的加速度. 如图所示为倾角为37°的斜面,一个质量1kg的滑块可以沿斜面匀速下滑,现将物块置于斜面的底端A点,用一水平向右的恒定推力F推动滑块,1s内滑块沿斜面上滑了1m,2s后撤去推力,滑块刚好能滑到斜面顶端,g=10m/s2,求:
如图所示为倾角为37°的斜面,一个质量1kg的滑块可以沿斜面匀速下滑,现将物块置于斜面的底端A点,用一水平向右的恒定推力F推动滑块,1s内滑块沿斜面上滑了1m,2s后撤去推力,滑块刚好能滑到斜面顶端,g=10m/s2,求: