题目内容
11. 如图所示,质量为m,电量为q的带正电的物体,在磁感应强度为B,方向垂直纸面向里的匀强磁场中,沿动摩擦因数为μ的水平面向左运动,则( )
如图所示,质量为m,电量为q的带正电的物体,在磁感应强度为B,方向垂直纸面向里的匀强磁场中,沿动摩擦因数为μ的水平面向左运动,则( )| A. | 若另加一个电场强度为$\frac{μ(mg+qvB)}{q}$,方向水平向右的匀强电场,物体做匀速运动 | |
| B. | 若另加一个电场强度为$\frac{mg+qvB}{q}$,方向竖直向上的匀强电场,物体做匀速直线运动 | |
| C. | 物体的速度由v减小到零所用的时间等于$\frac{mv}{μ(mg+qvB)}$ | |
| D. | 物体的速度由v减小到零所用的时间小于$\frac{mv}{μ(mg+qvB)}$ |
分析 对物体受力分析,受重力、支持力,洛伦兹力和滑动摩擦力;加电场力后,当受力平衡时做匀速直线运动.根据左手定则,洛伦兹力向下,根据动量定理或运动学的公式即可求解时间.
解答 解:A、对物体受力分析,受重力、支持力,洛伦兹力和滑动摩擦力;根据左手定则,洛伦兹力向下.
若另加一个水平向右的电场,电场力的方向向右,与摩擦力方向相同,合外力不为零,滑块不可能做匀速直线运动.故A错误;
B、若另加一个竖直向上的电场,电场力的方向向上,当qE=(mg+qvB),即E=$\frac{mg+qvB}{q}$时,支持力为零,摩擦力为零,则合外力为零,滑块可能做匀速直线运动.故B正确;
CD、由于合力向右,物体向左做减速运动;由于摩擦力f=μ(mg+qvtB),随速度的减小不断减小,摩擦力f不断减小,加速度不断减小,不是匀变速运动,故物体的速度由v减小到零所经历的时间t,由动量定理得
-ft=0-mv.
得 t=$\frac{mv}{f}$>$\frac{mv}{μ(mg+qvB)}$.故CD错误;
故选:B.
点评 本题关键是对物体受力分析,由于洛伦兹力随着速度变化,当受力平衡时洛伦兹力不变,做匀速直线运动.

练习册系列答案
相关题目
1.汽车拉着拖车前进,汽车对拖车的作用力大小为F,拖车对汽车的作用力大小为T.关于F与T的关系,下列说法正确的是( )
| A. | 汽车加速前进时F大于T | |
| B. | 汽车减速前进时F小于T | |
| C. | 只有汽车匀速前进时F才等于T | |
| D. | 无论汽车加速、减速还是匀速前进,F始终等于T |
19. 如图所示,两个质量均为m的小球A和B用轻质弹簧连接,静止放在光滑水平面上.现给小球A一速度v,在弹簧第一次被压缩到最短的过程中,下列说法正确的是( )
如图所示,两个质量均为m的小球A和B用轻质弹簧连接,静止放在光滑水平面上.现给小球A一速度v,在弹簧第一次被压缩到最短的过程中,下列说法正确的是( )
 如图所示,两个质量均为m的小球A和B用轻质弹簧连接,静止放在光滑水平面上.现给小球A一速度v,在弹簧第一次被压缩到最短的过程中,下列说法正确的是( )
如图所示,两个质量均为m的小球A和B用轻质弹簧连接,静止放在光滑水平面上.现给小球A一速度v,在弹簧第一次被压缩到最短的过程中,下列说法正确的是( )| A. | A、B两球的总动能不变 | |
| B. | A、B两球的总动量为mv | |
| C. | 弹簧对B球的作用力大于对A球的作用力 | |
| D. | 弹簧被压缩到最短时,A、B两球的总动能最小 |
3.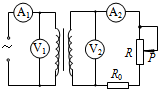 如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
 如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )| A. | V2示数变小 | B. | V1示数变大 | C. | A2示数变大 | D. | A1示数变小 |
20. 如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个用相同材料、相同粗细的导线绕制的单匝闭合正方形线圈l和2,其边长L1>L2,在距磁场上界面h高处由静止开始自由下落,再逐渐完全进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈l、2落地时的速度大小分别为v1、v2,在磁场中运动时产生的热世分别为Q1、Q1,通过线圈截面的电荷量分别为q1、q2,不计空气阻力,则( )
如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个用相同材料、相同粗细的导线绕制的单匝闭合正方形线圈l和2,其边长L1>L2,在距磁场上界面h高处由静止开始自由下落,再逐渐完全进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈l、2落地时的速度大小分别为v1、v2,在磁场中运动时产生的热世分别为Q1、Q1,通过线圈截面的电荷量分别为q1、q2,不计空气阻力,则( )
 如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个用相同材料、相同粗细的导线绕制的单匝闭合正方形线圈l和2,其边长L1>L2,在距磁场上界面h高处由静止开始自由下落,再逐渐完全进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈l、2落地时的速度大小分别为v1、v2,在磁场中运动时产生的热世分别为Q1、Q1,通过线圈截面的电荷量分别为q1、q2,不计空气阻力,则( )
如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个用相同材料、相同粗细的导线绕制的单匝闭合正方形线圈l和2,其边长L1>L2,在距磁场上界面h高处由静止开始自由下落,再逐渐完全进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈l、2落地时的速度大小分别为v1、v2,在磁场中运动时产生的热世分别为Q1、Q1,通过线圈截面的电荷量分别为q1、q2,不计空气阻力,则( )| A. | v1<v2,Q1>Q2,q1>q2 | B. | v1=v2,Q1=Q2,q1=q2 | ||
| C. | v1<v2,Q1>Q2,q1=q2 | D. | v1=v2,Q1<Q2,q1<q2 |
1.在一次观察光的衍射实验中,观察到如图所示的清晰的亮暗相间的图样,那么障碍物是下列给出的 ( )


| A. | 很小的不透明圆板 | B. | 很大的中间有大圆孔的不透明挡板 | ||
| C. | 很大的不透明圆板 | D. | 很大的中间有小圆孔的不透明挡板 |
 如图所示,水平轨道左端与长L=1.25m的水平传送带相接,传送带逆时针匀速运动的速度υ0=1m/s.轻弹簧右端固定在光滑水平轨道上,弹簧处于自然状态时左端恰位于A点.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板上掉下.竖直半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,g取10m/s2.求:
如图所示,水平轨道左端与长L=1.25m的水平传送带相接,传送带逆时针匀速运动的速度υ0=1m/s.轻弹簧右端固定在光滑水平轨道上,弹簧处于自然状态时左端恰位于A点.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板上掉下.竖直半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,g取10m/s2.求: