题目内容
13. 如图所示装置可绕竖直轴O′O转动,可视为质点的小球A于两细线连接后分别系于B、C两点,当细线AB沿水平方向绷直时,细线AC与竖直方向的夹角θ=53°.已知小球的质量m=1kg,细线AC长L=3m.(重力加速度取g=10m/s2,sin53°=0.8)
如图所示装置可绕竖直轴O′O转动,可视为质点的小球A于两细线连接后分别系于B、C两点,当细线AB沿水平方向绷直时,细线AC与竖直方向的夹角θ=53°.已知小球的质量m=1kg,细线AC长L=3m.(重力加速度取g=10m/s2,sin53°=0.8)(1)若装置匀速转动时,细线AB刚好被拉至成水平状态,求此时的角速度ω1.
(2)若装置匀速转动的角速度ω2=$\sqrt{\frac{65}{9}}$rad/s,求细线AB和AC上的张力大小TAB、TAC.
分析 (1)当细线AB刚好被拉直,则AB的拉力为零,靠AC的拉力和重力的合力提供向心力,结合牛顿第二定律求出此时的角速度.
(2)抓住小球竖直方向上的合力为零,水平方向上的合力提供向心力,结合牛顿第二定律求出细线AB和AC的张力.
解答 解:(1)当细线AB刚好被拉直,则AB的拉力为零,靠AC的拉力和重力的合力提供向心力,
根据牛顿第二定律有:$mgtan37°=m{L}_{AB}{{ω}_{1}}^{2}$,
解得${ω}_{1}=\sqrt{\frac{gtan53°}{{L}_{AB}}}=\sqrt{\frac{10×\frac{4}{3}}{3×\frac{4}{5}}}=\frac{5\sqrt{2}}{3}rad/s$.
(2)若装置匀速转动的角速度ω2=$\sqrt{\frac{65}{9}}$rad/s,
竖直方向上有:TACcos53°=mg,
水平方向上有:${T}_{AC}sin53°+{T}_{AB}=m{L}_{AB}{{ω}_{2}}^{2}$,
代入数据解得TAC=$\frac{50}{3}$N,TAB=4N.
答:(1)此时的角速度为$\frac{5\sqrt{2}}{3}$rad/s.
(2)细线AB和AC上的张力大小TAB、TAC分别为4N、$\frac{50}{3}$N.
点评 解决本题的关键知道小球向心力的来源,抓住临界状态,结合牛顿第二定律进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.运动员用双手握住竖直的竹竿匀速攀上和匀速下滑时,运动员所受的摩擦力分别是f1和 f2,那么下列判断正确的是( )
| A. | f1向下,f2向下,且f1=f2 | B. | f1向下,f2向上,且f1=f2 | ||
| C. | f1向上,f2向上,且f1=f2 | D. | f1向上,f2向下,且f1=f2 |
1.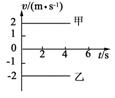 如图所示为甲、乙两质点运动的v-t图象.对于甲、乙两质点的运动情况,下列说法中正确的是 ( )
如图所示为甲、乙两质点运动的v-t图象.对于甲、乙两质点的运动情况,下列说法中正确的是 ( )
 如图所示为甲、乙两质点运动的v-t图象.对于甲、乙两质点的运动情况,下列说法中正确的是 ( )
如图所示为甲、乙两质点运动的v-t图象.对于甲、乙两质点的运动情况,下列说法中正确的是 ( )| A. | 两个质点运动的速度相同 | |
| B. | 两个质点的运动方向相反 | |
| C. | 相同时间内,两质点运动的位移相同 | |
| D. | 若两质点同时从同一地点出发,它们间的距离会越来越大 |
8. 如图所示,在水平桌面上固定着一个光滑圆轨道,A、B、C、D四点为圆轨道的四等分点,E点是CD弧的中点,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度v0逆时针运动,与乙球发生第一次碰撞后,恰好在E点发生第二次碰撞则甲、乙两球的质量之比为( )
如图所示,在水平桌面上固定着一个光滑圆轨道,A、B、C、D四点为圆轨道的四等分点,E点是CD弧的中点,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度v0逆时针运动,与乙球发生第一次碰撞后,恰好在E点发生第二次碰撞则甲、乙两球的质量之比为( )
 如图所示,在水平桌面上固定着一个光滑圆轨道,A、B、C、D四点为圆轨道的四等分点,E点是CD弧的中点,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度v0逆时针运动,与乙球发生第一次碰撞后,恰好在E点发生第二次碰撞则甲、乙两球的质量之比为( )
如图所示,在水平桌面上固定着一个光滑圆轨道,A、B、C、D四点为圆轨道的四等分点,E点是CD弧的中点,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度v0逆时针运动,与乙球发生第一次碰撞后,恰好在E点发生第二次碰撞则甲、乙两球的质量之比为( )| A. | 3:13 | B. | 3:7 | C. | 11:5 | D. | 10:3 |
5. 图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )
图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )
 图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )
图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )| A. | 50V | B. | 25$\sqrt{3}$V | C. | 25$\sqrt{2}$ | D. | 25V |
2.行驶的汽车通过下列路段时,不需要向心力的是( )
| A. | 水平直道 | B. | 水平弯道 | C. | 凹形路面 | D. | 拱形桥面 |

 如图所示,物体在离斜面底端L处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,水平面足够长,动摩擦因数为0.5.若斜面是光滑的,物体在水平面上滑行的距离为s1;若斜面粗糙,动摩擦因数也为0.5,物体在水平面上滑行的距离为s2.斜面倾角为37°,求s1:s2为多少?(已知sin37°=0.6,cos37°=0.8)
如图所示,物体在离斜面底端L处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,水平面足够长,动摩擦因数为0.5.若斜面是光滑的,物体在水平面上滑行的距离为s1;若斜面粗糙,动摩擦因数也为0.5,物体在水平面上滑行的距离为s2.斜面倾角为37°,求s1:s2为多少?(已知sin37°=0.6,cos37°=0.8)