题目内容
8. 如图所示,在水平桌面上固定着一个光滑圆轨道,A、B、C、D四点为圆轨道的四等分点,E点是CD弧的中点,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度v0逆时针运动,与乙球发生第一次碰撞后,恰好在E点发生第二次碰撞则甲、乙两球的质量之比为( )
如图所示,在水平桌面上固定着一个光滑圆轨道,A、B、C、D四点为圆轨道的四等分点,E点是CD弧的中点,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度v0逆时针运动,与乙球发生第一次碰撞后,恰好在E点发生第二次碰撞则甲、乙两球的质量之比为( )| A. | 3:13 | B. | 3:7 | C. | 11:5 | D. | 10:3 |
分析 两球碰撞过程遵守动量守恒和机械能守恒,由动量守恒定律和机械能守恒定律分别列方程得到碰撞后速度关系式,再由圆周知识确定碰撞后速度大小之比,再求解质量之比.
解答 解:设碰撞后m1、m2的速度大小分别为v1、v2.由题分析得到,m1碰后可能反向.以v0方向为正,由动量守恒定律得:
m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,在相同时间内,线速度大小与路程成正比,则有:
v1:v2=225°:135°=5:3 ②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:$\frac{1}{2}$m1v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22…③
将②代人①③得:m1:m2=3:13
m1碰后也可能方向不变.以v0方向为正,由动量守恒定律得:
m1v0=m2v2+m1v1…④
因为恰在C点发生第二次碰撞,在相同时间内,线速度大小与路程成正比,则有:
v1:v2=135°:(135°+360°)=5:3…⑤
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:$\frac{1}{2}$m1v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22…③
联立③④⑤得:m1:m2=11:5
故选:AC
点评 解决本题时,要明确碰撞遵守动量守恒和机械能守恒.关键是根据圆周运动知识的规律研究碰撞后速度的关系,要注意选择正方向.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
14.下列现象中,能用离心现象解释的是( )
| A. | 拍掉衣服表面的灰尘 | |
| B. | 洗衣机的脱水筒把衣服上的水脱干 | |
| C. | 用手把温度计中的水银柱甩回玻璃泡内 | |
| D. | 匀速直线运动的公共汽车急刹车时,乘客都向前倾倒 |
19.氢原子的核外电子由离原子核较远的轨道跃迁到离核较近的轨道上时,下列说法中正确的是( )
| A. | 氢原子的能量增加 | B. | 核外电子的动能减小 | ||
| C. | 氢原子要吸收一定频率的光子 | D. | 氢原子要放出一定频率的光子 |
16. 从距墙壁为5m处以某一初速度垂直墙壁抛出个小球,在与墙壁相碰后弹回,返回到距墙壁2m处被接住.如图所示.则这一过程中 ( )
从距墙壁为5m处以某一初速度垂直墙壁抛出个小球,在与墙壁相碰后弹回,返回到距墙壁2m处被接住.如图所示.则这一过程中 ( )
 从距墙壁为5m处以某一初速度垂直墙壁抛出个小球,在与墙壁相碰后弹回,返回到距墙壁2m处被接住.如图所示.则这一过程中 ( )
从距墙壁为5m处以某一初速度垂直墙壁抛出个小球,在与墙壁相碰后弹回,返回到距墙壁2m处被接住.如图所示.则这一过程中 ( )| A. | 小球的位移大小为3m,方向水平向右,路程为7m | |
| B. | 小球的位移大小为7m,方向水平向左,路程为7m | |
| C. | 小球的位移大小为3m,方向水平向右,路程为3m | |
| D. | 小球的位移大小为7m,方向水平向左,路程为3m |
3. (单选)通过重物自由下落“验证机械能守恒定律”的实验装置如图所示.为完成此实验,除了图中所示的器材,还必须用的器材有( )(选填下列器材的代码).
(单选)通过重物自由下落“验证机械能守恒定律”的实验装置如图所示.为完成此实验,除了图中所示的器材,还必须用的器材有( )(选填下列器材的代码).
 (单选)通过重物自由下落“验证机械能守恒定律”的实验装置如图所示.为完成此实验,除了图中所示的器材,还必须用的器材有( )(选填下列器材的代码).
(单选)通过重物自由下落“验证机械能守恒定律”的实验装置如图所示.为完成此实验,除了图中所示的器材,还必须用的器材有( )(选填下列器材的代码).| A. | 毫米刻度尺 | B. | 秒表 | C. | 天平 | D. | 直流电源 |
20.运动员在百米赛跑中,1秒末测得的速度为9m/s,到达50m处的速度为9.2m/s,10秒末到达终点时的速度为10.2m/s,则运动员在全路程中的平均速度为( )
| A. | 9m/s | B. | 9.2m/s | C. | 10m/s | D. | 10.2m/s |
17. 我国发射的“神州六号”载人飞船,与“神州五号”飞船相比,它在更高的轨道上绕地球做匀速圆周运动,如图所示,下列说法中正确的是 ( )
我国发射的“神州六号”载人飞船,与“神州五号”飞船相比,它在更高的轨道上绕地球做匀速圆周运动,如图所示,下列说法中正确的是 ( )
 我国发射的“神州六号”载人飞船,与“神州五号”飞船相比,它在更高的轨道上绕地球做匀速圆周运动,如图所示,下列说法中正确的是 ( )
我国发射的“神州六号”载人飞船,与“神州五号”飞船相比,它在更高的轨道上绕地球做匀速圆周运动,如图所示,下列说法中正确的是 ( )| A. | “神州六号”的速度较小 | |
| B. | “神州六号”的周期更短 | |
| C. | “神州六号”的速度与“神州五号”的相同 | |
| D. | “神州六号”的周期与“神州五号”的相同 |
 如图所示装置可绕竖直轴O′O转动,可视为质点的小球A于两细线连接后分别系于B、C两点,当细线AB沿水平方向绷直时,细线AC与竖直方向的夹角θ=53°.已知小球的质量m=1kg,细线AC长L=3m.(重力加速度取g=10m/s2,sin53°=0.8)
如图所示装置可绕竖直轴O′O转动,可视为质点的小球A于两细线连接后分别系于B、C两点,当细线AB沿水平方向绷直时,细线AC与竖直方向的夹角θ=53°.已知小球的质量m=1kg,细线AC长L=3m.(重力加速度取g=10m/s2,sin53°=0.8)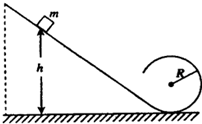 如图所示,位于竖直平面内的光滑轨道,由一段斜的轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.
如图所示,位于竖直平面内的光滑轨道,由一段斜的轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.