题目内容
4. 如图所示,在足够长的光滑绝缘水平直线轨道上方的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点的检验电荷),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),P到物块的重心竖直距离为h,P、A连线与水平轨道的夹角为60°,k为静电常数,下列说法正确的是( )
如图所示,在足够长的光滑绝缘水平直线轨道上方的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点的检验电荷),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),P到物块的重心竖直距离为h,P、A连线与水平轨道的夹角为60°,k为静电常数,下列说法正确的是( )| A. | 物块在A点的电势能EPA=+Qφ | |
| B. | 物块在A点时受到轨道的支持力大小为mg+$\frac{3\sqrt{3}kQq}{8{h}^{2}}$ | |
| C. | 点电荷+Q产生的电场在B点的电场强度大小EB=$k\frac{Q}{h}$ | |
| D. | 点电荷+Q产生的电场在B点的电势φB=$\frac{m}{2q}$(v02-v2)+φ |
分析 对物体进行受力分析,受重力、支持力、库仑力,根据竖直方向合力等于零,求出物体在A点受到轨道的支持力.从A点到B点,只有电场力做功,根据动能定理,求出电场力做功,从而得出两点间的电势差,从而得出B点的电势.
解答 解:A、物块在A点的电势能EPA=+qφ,则A错误
B、物体受到点电荷的库仑力为:F=$K\frac{Qq}{{r}^{2}}$
由几何关系可知:r=$\frac{h}{sin60°}$
设物体在A点时受到轨道的支持力大小为N,由平衡条件有:
N-mg-Fsin60°=0
解得:N=mg+$\frac{3\sqrt{3}kQq}{8{h}^{2}}$.B正确;
C、点电荷+Q产生的电场在B点的电场强度大小EB=$K\frac{Q}{{r}^{2}}$
D、设点电荷产生的电场在B点的电势为φB,动能定理有:$-q(φ-{φ}_{B})=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得:φB=$\frac{m}{2q}$(v02-v2)+φ.故D正确
故选:BD
点评 解决本题的关键知道电场力做功W=qU,U等于两点间的电势差.以及掌握库仑定律和动能定理的运用.

练习册系列答案
相关题目
15. 如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )
如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )
 如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )
如图所示,真空中有两个固定的点电荷,Q1带正电,Q2带负电,其电荷量Q1<Q2.现将一试探电荷q置于Q1、Q2连线所在的直线上,使q处于平衡状态.不计重力.则( )| A. | q一定是正电荷 | B. | q一定是负电荷 | C. | q离Q1比离Q2近 | D. | q离Q1比离Q2远 |
19. 如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )
如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )
 如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )
如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )| A. | mgh-$\frac{1}{2}$mv2 | B. | $\frac{1}{2}$mv2-mgh | C. | -mgh | D. | -(mgh+$\frac{1}{2}$mv2) |
9.汽车转弯时向心力由什么力提供( )
| A. | 支持力 | B. | 滑动摩擦力 | C. | 静摩擦力 | D. | 重力 |
13.下列说法正确的是( )
| A. | 物体从外界吸收热量,其内能一定增加 | |
| B. | 热机的效率可以达到100% | |
| C. | 叶面上的小露珠呈球形是由于液体表面张力的作用 | |
| D. | 布朗运动是悬浮颗粒分子的无规则运动 |
 如图所示,一小型发电机内有100匝矩形线圈,线圈面积S=0.10m2,电阻r=1Ω,其它导线电阻不计.现让矩形线圈在B=0.2T的匀强磁场中,以恒定的角速度ω=50πrad/s绕垂直于磁场方向的固定轴OO′匀速转动,发电机线圈两端与R=99Ω的电阻构成闭合回路.求:
如图所示,一小型发电机内有100匝矩形线圈,线圈面积S=0.10m2,电阻r=1Ω,其它导线电阻不计.现让矩形线圈在B=0.2T的匀强磁场中,以恒定的角速度ω=50πrad/s绕垂直于磁场方向的固定轴OO′匀速转动,发电机线圈两端与R=99Ω的电阻构成闭合回路.求: 如图所示,是一静电场的一部分电场线的分布,图中A、B为电场中的两点.由图可知,电场强度EA大于EB,电势φA小于φB.若将一个负电荷分别置于A、B两点,具有的电势能EPA大于EPB(填“大于”、“小于”或“等于”)
如图所示,是一静电场的一部分电场线的分布,图中A、B为电场中的两点.由图可知,电场强度EA大于EB,电势φA小于φB.若将一个负电荷分别置于A、B两点,具有的电势能EPA大于EPB(填“大于”、“小于”或“等于”)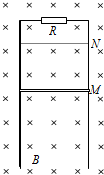 如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻,将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.
如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻,将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.