题目内容
19.“嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一步.已知“嫦娥一号”绕月飞行轨道近似圆周,距月球表面高度为H,飞行周期为T,月球的半径为R,引力常量为G,试求:(1)月球的质量M
(2)月球表面的重力加速度g0.
分析 “嫦娥一号”围绕月球做圆周运动过程中,月球对“嫦娥一号”的万有引和提供“嫦娥一号”的向心力,由此列式可以求出月球的质量M;在月球表面,月球对物体的万有引力等于月球表面的重力,由此列式得出月球表面的重力加速度g0.
解答 解:(1)由题意,嫦娥一号由万有引力提供向心力,设嫦娥一号的质量为m,月球的质量为M,因为轨道高度为H,则轨道半径r=R+H,根据万有引力提供向心力得:
$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,
r=R+H,
得月球的质量:
$M=\frac{4{π}^{2}(R+H)^{3}}{G{T}^{2}}$.
(2)月球表面的重力和万有引力相等,即有:$G\frac{Mm}{{R}^{2}}=m{g}_{0}$,
解得:${g}_{0}=\frac{GM}{{R}^{2}}=\frac{4{π}^{2}{(R+H)}^{3}}{{R}^{2}{T}^{2}}$.
答:(1)月球的质量$\frac{4{π}^{2}{(R+H)}^{3}}{G{T}^{2}}$.(2)月球表面的重力加速度$\frac{4{π}^{2}{(R+H)}^{3}}{{R}^{2}{T}^{2}}$.
点评 能正确根据卫星运动时的向心力由万有引力提供和量球表面的重力和万有引力相等列式求解有关质量、重力加速度问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.甲、乙、丙三个物体,甲放在广州,乙放在上海,丙放在北京,当它们与地球一起转动时( )
| A. | 角速度甲最大,线速度乙最小 | |
| B. | 三物体的角速度、周期一样,线速度丙最小 | |
| C. | 角速度丙最小,线速度甲最大 | |
| D. | 三物体的角速度、线速度和周期都相等 |
4.关于万有引力表达式F=$\frac{GMm}{r}$的说法正确的是( )
| A. | 表达式中G是引力常量是由卡文迪许推导并人为规定的 | |
| B. | 当r趋于0时两物体间的万有引力趋于无穷大 | |
| C. | M、m所受万有引力大小相等时是一对相互作用力 | |
| D. | 质量大的物体所受万有引力比质量小的大 |
8.下列运动能满足机械能守恒的是( )
| A. | 石头从手中抛出后的运动(不计空气阻力) | |
| B. | 子弹射穿木块 | |
| C. | 吊车将货物匀速吊起 | |
| D. | 降落伞在空中匀速下降 |
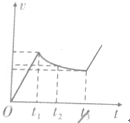
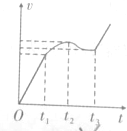
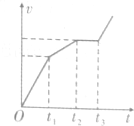
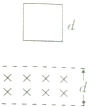 如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
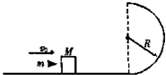 如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以v0=400m/s的水平速度射入木块中,然后一起运动到轨道最高点水平抛出(g取10m/s2),求:
如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以v0=400m/s的水平速度射入木块中,然后一起运动到轨道最高点水平抛出(g取10m/s2),求: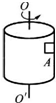 如图所示,半径为r的圆筒绕竖直中心轴OO′转动,小物块A靠在圆筒的内壁上,它与圆筒的静摩擦因数为μ,现要使A不下落,则圆筒转动的转速至少应为$\frac{{\sqrt{ug}}}{{\sqrt{4r{π^2}}}}$.
如图所示,半径为r的圆筒绕竖直中心轴OO′转动,小物块A靠在圆筒的内壁上,它与圆筒的静摩擦因数为μ,现要使A不下落,则圆筒转动的转速至少应为$\frac{{\sqrt{ug}}}{{\sqrt{4r{π^2}}}}$. 如图所示的皮带传动装置中,右边两轮是连在一起同轴转动,图中三轮半径的关系为:R1=2R2,R3=$\frac{3}{2}$R1,A、B、C三点为三个轮边缘上的点,皮带不打滑,则A、B、C三点的线速度之比为1:1:3,角速度之比为1:2:2,周期之比为2:1:1.
如图所示的皮带传动装置中,右边两轮是连在一起同轴转动,图中三轮半径的关系为:R1=2R2,R3=$\frac{3}{2}$R1,A、B、C三点为三个轮边缘上的点,皮带不打滑,则A、B、C三点的线速度之比为1:1:3,角速度之比为1:2:2,周期之比为2:1:1.