题目内容
1.将两质点在空间同一点处同时水平反向抛出,已知重力加速度为g.若抛出时的速率同为v,当两个质点位移相互垂直时它们之间的距离为$\frac{4{v}^{2}}{g}$;若抛出时的速率分别为v1和v2,当两个质点速度相互垂直时它们之间的距离为(v1+v2)$\frac{\sqrt{{v}_{1}{v}_{2}}}{g}$.分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,当两个质点位移相互垂直时,即两个质点的位移与竖直方向上的夹角之和为90°,根据位移关系求出运动的时间,从而求出它们之间的距离.当两个质点的速度方向互相垂直时,知两个质点速度与竖直方向上的夹角之和为90°,根据竖直分速度的关系求出运动的时间,从而求出两质点的水平位移,从而求出两水平位移之和.
解答 解:(1)设下落t时间,两位移垂直时与水平方向的夹角分别为45°.
则tan45°=$\frac{\frac{1}{2}g{t}^{2}}{vt}$=$\frac{gt}{2v}$,t=$\frac{2v}{g}$,落地前两质点位移方向互相垂直时,根据运动的独立性,它们之间的距离为水平位移之和 x=2vt=$\frac{4{v}^{2}}{g}$
(2)设下落时间为t,两速度垂直时与水平方向的夹角分别为α、β,则:
tanα=$\frac{gt}{{v}_{1}}$,tanβ=$\frac{gt}{{v}_{2}}$
落地前两个质点的速度方向互相垂直时
则tanα•tanβ=1
解得t=$\frac{\sqrt{{v}_{1}{v}_{2}}}{g}$
水平距离 s=(v1+v2)t
=(v1+v2)$\frac{\sqrt{{v}_{1}{v}_{2}}}{g}$
答:(1)当两个质点速度相互垂直时
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
12.如图所示,甲、乙传送带倾斜放置,并以相同的恒定速率v逆时针运动,两传送带粗糙程度不同,但长度、倾角均相同.将一小物体分别从两传送带顶端的A点无初速释放,甲传送带上小物体到达底端B点时恰好达到速度v,乙传送带上小物体到达传送带中部的C点时恰好达到速度v,接着以速度v运动到底端B点.则小物体从A运动到B的过程中( )


| A. | 小物体与甲传送带之间的动摩擦因数比与乙之间的小 | |
| B. | 两传送带对小物体做功相等 | |
| C. | 物体在甲传送带上的重力做功的平均功率比在乙上的大 | |
| D. | 两传送带因与小物体摩擦产生的热量相等 |
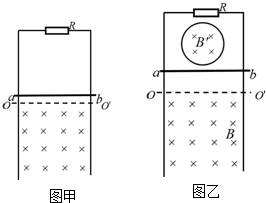
9.在如图甲所示的电路中,L1、L2和L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.当开关S闭合后,电路中的总电流为0.25A,则此时( )


| A. | 通过L1的电流为L2电流的2倍 | B. | 此时L1、L2和L3的电阻均为12Ω | ||
| C. | L1消耗的电功率为0.75 W | D. | L1消耗的电功率为L2电功率的4倍 |
16.如图装置,不计滑轮的质量和绳与滑轮间的摩擦,整个装置处于平衡,则( )
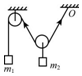

| A. | m1>$\frac{1}{2}$m2 | |
| B. | m1<$\frac{1}{2}$m2 | |
| C. | 若使m1的质量逐渐增加一些,整个装置一定能达到的平衡 | |
| D. | 若将右边绳子悬点O向右平移一些,则重物m2将会下降一些 |
13.辨别物质是晶体还是非晶体,比较正确的方法是( )
| A. | 从外形来判断 | B. | 从各向异性或各向同性来判断 | ||
| C. | 从导电性能来判断 | D. | 从是否具有确定的熔点来判断 |
10.一个做直线运动的物体,在t=5s内通过的位移是s=70m,这个物体5s内的平均速度是( )
| A. | 14m∕s | B. | 15m∕s | C. | 6m∕s | D. | 无法确定 |