题目内容
14. 如图所示,以9.8m/s的水平速度V0抛出的物体,飞行一段时间后垂直地撞在倾角为θ=30°的斜面上,可知物体完成这段飞行的时间是$\sqrt{3}$s,下落高度14.7m.
如图所示,以9.8m/s的水平速度V0抛出的物体,飞行一段时间后垂直地撞在倾角为θ=30°的斜面上,可知物体完成这段飞行的时间是$\sqrt{3}$s,下落高度14.7m.
分析 小球垂直地撞在倾角θ为30°的斜面上,知小球的速度方向与斜面垂直,将该速度进行分解,根据水平方向上的速度求出竖直方向上的分速度,根据分运动公式列式求解时间和竖直分位移.
解答 解:小球撞在斜面上的速度与斜面垂直,将该速度分解,如图:
则tan60°=$\frac{{v}_{y}}{{v}_{0}}$,则vy=v0tan60°=gt,所以:
t=$\frac{\sqrt{3}{v}_{0}}{g}$=$\frac{9.8\sqrt{3}}{9.8}$=$\sqrt{3}$s;
下落的高度:
h=$\frac{1}{2}g{t}^{2}$=$\frac{1}{2}×9.8×3$=14.7m;
故答案为:$\sqrt{3}$s,14.7m.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,根据竖直方向上的分速度规律求出运动的时间和高度,基础题目.

练习册系列答案
相关题目
5.两个完全相同的电热器,分别通有如图A、B所示的交流电流,则它们的功率之比为( )


| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
2.在下列几种运动中遵守机械守恒定律的是( )
| A. | 雨点匀速下落 | |
| B. | 自由落体运动 | |
| C. | 汽车刹车时的运动 | |
| D. | 在光滑水平面上弹簧振子所做的简谐振动 |
9.有一宇宙飞船到了某行星上(该行星没有自转运动),以速度v接近行星赤道表面匀速飞行,测出运动的周期为T,已知引力常量为G,则可得( )
| A. | 该行星的半径为$\frac{πvT}{2}$ | B. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | ||
| C. | 无法测出该行星的质量 | D. | 该行星表面的重力加速度为$\frac{2v}{T}$ |
4. 如图所示,质量为m的物体以速度v0离开桌面后,经过A点时所具有的机械能是(以地面为零势能面,不计空气阻力)( )
如图所示,质量为m的物体以速度v0离开桌面后,经过A点时所具有的机械能是(以地面为零势能面,不计空气阻力)( )
 如图所示,质量为m的物体以速度v0离开桌面后,经过A点时所具有的机械能是(以地面为零势能面,不计空气阻力)( )
如图所示,质量为m的物体以速度v0离开桌面后,经过A点时所具有的机械能是(以地面为零势能面,不计空气阻力)( )| A. | $\frac{1}{2}$mv02+mgh | B. | $\frac{1}{2}$mv02+mgH | C. | $\frac{1}{2}$mv02+mg(H-h) | D. | $\frac{1}{2}$mv02 |
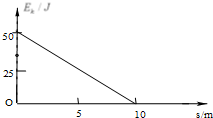 质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m.
质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m. 倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接,连接处用一光滑小圆弧过渡,斜面上距水平面高度分别为h1=5m和h2=0.2m的两点上,各固定一小球A和B.某时刻由静止开始释放A球,经过一段时间t后,同样由静止开始释放B球.g取10m/s2,则:
倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接,连接处用一光滑小圆弧过渡,斜面上距水平面高度分别为h1=5m和h2=0.2m的两点上,各固定一小球A和B.某时刻由静止开始释放A球,经过一段时间t后,同样由静止开始释放B球.g取10m/s2,则: 用三棱镜做测定玻璃折射率的实验,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2,然后在棱镜的另一侧观察,调整视线,使P2的像挡住P1的像,接着在眼睛所在的一侧插两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3和P1、P2的像.在纸上标出大头针位置的三棱镜如图所示:
用三棱镜做测定玻璃折射率的实验,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2,然后在棱镜的另一侧观察,调整视线,使P2的像挡住P1的像,接着在眼睛所在的一侧插两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3和P1、P2的像.在纸上标出大头针位置的三棱镜如图所示: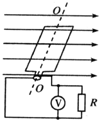 如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,此线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度为ω=2$\sqrt{2}$rad/s,外电路电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,此线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度为ω=2$\sqrt{2}$rad/s,外电路电阻R=4Ω,求: