题目内容
5.地球的第一宇宙速度为7.9km/s,地球表面的重力加速度为9.8m/s2,某行星的质量是地球的6倍,半径是地球的1.5倍,该行星的第一宇宙速度为15.8km/s,该行星表面的重力加速度为26.1m/s2.分析 第一宇宙速度是卫星绕星近表面速度,根据地球对卫星的万有引力提供向心力求解得第一宇宙速度公式$v=\sqrt{\frac{GM}{R}}$.
根据万有引力等于重力表示出星球表面重力加速度$g=G\frac{M}{{R}_{\;}^{2}}$进行求解.
解答 解:根据第一宇宙速度的公式有:$v=\sqrt{\frac{GM}{R}}$
得:$\frac{{v}_{行}^{\;}}{{v}_{地}^{\;}}=\sqrt{\frac{{M}_{行}^{\;}}{{M}_{地}^{\;}}\frac{{R}_{地}^{\;}}{{R}_{行}^{\;}}}=\sqrt{\frac{6}{1}×\frac{1}{1.5}}=2$
解得:${v}_{行}^{\;}=2{v}_{地}^{\;}=2×7.9km/s=15.8km/s$
根据重力加速度公式有:$g=G\frac{M}{{R}_{\;}^{2}}$
$\frac{{g}_{行}^{\;}}{{g}_{地}^{\;}}=\frac{{M}_{行}^{\;}}{{M}_{地}^{\;}}×\frac{{R}_{地}^{2}}{{R}_{行}^{2}}=\frac{6}{1}×\frac{{1}_{\;}^{2}}{1.{5}_{\;}^{2}}=\frac{8}{3}$
解得:${g}_{行}^{\;}=\frac{8}{3}{g}_{地}^{\;}=\frac{8}{3}×9.8=26.1m/{s}_{\;}^{2}$
故答案为:15.8,26.1
点评 根据万有引力提供圆周运动向心力求得星球第一宇宙速度的表达式,再根据已知质量和半径关系求出星球的第一宇宙速度.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
8. 如图所示,水平地面上有P、Q两点,A点和B点分别在P点和Q点的正上方,距离地面高度分别为h1和h2.某时刻在A点以速度v1水平抛出一小球,同时另一球从B点以速度v2水平抛出,结果两球落在P、Q连线上的O点,则有( )
如图所示,水平地面上有P、Q两点,A点和B点分别在P点和Q点的正上方,距离地面高度分别为h1和h2.某时刻在A点以速度v1水平抛出一小球,同时另一球从B点以速度v2水平抛出,结果两球落在P、Q连线上的O点,则有( )
 如图所示,水平地面上有P、Q两点,A点和B点分别在P点和Q点的正上方,距离地面高度分别为h1和h2.某时刻在A点以速度v1水平抛出一小球,同时另一球从B点以速度v2水平抛出,结果两球落在P、Q连线上的O点,则有( )
如图所示,水平地面上有P、Q两点,A点和B点分别在P点和Q点的正上方,距离地面高度分别为h1和h2.某时刻在A点以速度v1水平抛出一小球,同时另一球从B点以速度v2水平抛出,结果两球落在P、Q连线上的O点,则有( )| A. | 两个小球同时落地 | B. | 从B点抛出的小球先落地 | ||
| C. | PO:OQ=v1:v2 | D. | v1一定大于v2 |
16.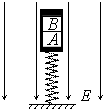 如图所示,质量均为m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现加上竖直向下的匀强电场,场强大小为$\frac{mg}{2q}$,当运动距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )
如图所示,质量均为m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现加上竖直向下的匀强电场,场强大小为$\frac{mg}{2q}$,当运动距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )
 如图所示,质量均为m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现加上竖直向下的匀强电场,场强大小为$\frac{mg}{2q}$,当运动距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )
如图所示,质量均为m的A、B两物体叠放在劲度系数为k的竖直轻质弹簧上并保持静止,其中B带负电,电荷量大小为q,A始终不带电.现加上竖直向下的匀强电场,场强大小为$\frac{mg}{2q}$,当运动距离h时B与A分离.从开始运动到B和A刚分离的过程中,下列说法正确的是( )| A. | B对A的压力一直减小 | B. | B物体的动能一直增加 | ||
| C. | 物体B机械能的增加量为$\frac{mgh}{2}$ | D. | 两物体运动的距离h=$\frac{3mg}{2k}$ |
13. 用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )
用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )
 用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )
用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )| A. | 如果小球每一次都从同一点无初速释放,重复几次的落点落在同一位置 | |
| B. | 由于偶然因素存在,重复操作时小球的落点不重合是正常的,但落点应当比较密集 | |
| C. | 测定P点位置时,如果重复10次的落点分别为P1、P2、P3、…P10,则OP应取OP1、OP2、OP3…OP10的平均值,即OP=$\frac{1}{10}$(OP1+OP2+…+OP10的) | |
| D. | 用半径尽量小的圆把P1、P2、P3…P10圈住,这个圆的圆心就是入射球落点的平均位置P |
20.下列说法正确的是( )
| A. | 液晶具有流动性,光学性质各向异性 | |
| B. | 气体扩散现象表明气体分子间存在斥力 | |
| C. | 热量总是自发的从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 机械能不可能全部转化为内能,内能也无法全部用来做功以转化成机械能 |
 在研究电磁感应现象的实验中所用的器材如图所示.它们是:①电流计②直流电源③带铁芯的线圈A④线圈B⑤电键⑥滑动变阻器
在研究电磁感应现象的实验中所用的器材如图所示.它们是:①电流计②直流电源③带铁芯的线圈A④线圈B⑤电键⑥滑动变阻器 质量为m=1kg的物体,在竖直平面内高h=1m的光滑弧形轨道A点,以v0=4m/s的初速度沿轨道滑下,并进入BC轨道,最后停在C点,如图所示.(取g=10m/s2) 求:
质量为m=1kg的物体,在竖直平面内高h=1m的光滑弧形轨道A点,以v0=4m/s的初速度沿轨道滑下,并进入BC轨道,最后停在C点,如图所示.(取g=10m/s2) 求: 如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.
如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.