题目内容
6. (1)带负电的两个点电荷AB固定在相距10cm的地方,如果将第三个点电荷C放在AB连线间距A为2cm的地方,C恰好静止不动,则A、B两个点电荷的电荷量之比为1:16;AB之间距A为2cm处的电场强度E=0.
(1)带负电的两个点电荷AB固定在相距10cm的地方,如果将第三个点电荷C放在AB连线间距A为2cm的地方,C恰好静止不动,则A、B两个点电荷的电荷量之比为1:16;AB之间距A为2cm处的电场强度E=0.(2)实线为电场线,虚线为等势面,且相邻等势面间的电势差相等,正电荷在等势面φ3上时,具有动能20J,它运动到等势面φ1上时,动能为零.令φ2=0,那么,当该电荷的电势能为4J时,求它的动能是6焦耳.
分析 (1)对放入电荷受力分析,根据平衡条件对“放入的电荷处于平衡状态”这一特点进行受力分析即可:
(2)相邻等势面间的电势差相等,电荷经过相邻等势面时电场力做功相等,根据动能定理求出电荷经经过φ2等势面时的动能,确定电荷总能量,再由能量守恒定律求出电势能为4J时它的动能.
解答 解:(1)因为QA、QB为固定的负点电荷,只要放入的点电荷受到的合力为0即可,通过受力分析可知,既可以放入正电荷,也可以放入负电荷,由于C恰好处于平衡状态,所以C点电荷在两个固定的电荷之间.
由库仑定律得,对C点电荷,
则有:k$\frac{{Q}_{A}q}{{2}^{2}}$=k$\frac{{Q}_{B}q}{(10-2)^{2}}$
所以:$\frac{{Q}_{A}}{{Q}_{B}}$=$\frac{{2}^{2}}{{8}^{2}}$=$\frac{1}{16}$
粒子受到的电场力的合力为零,故场强为零;
(2)由题,正电荷在等势面φ3上时动能20J,在等势面φ1上时动能为零,动能的减小为20J.由于相邻等势面间的电势差相等,电荷经过相邻等势面时电场力做功相等,动能减小量相等,则电荷经经过φ2等势面时的动能为10J,又φ2=0,所以电荷的动能与电势能的总量为10J,根据能量守恒定律得到,电势能为4J时它的动能为6J.
故答案为:(1)1:16;0 (2)6
点评 (1)本题考察了库仑定律在电荷平衡中的应用,本题的难点在于计算,学生列出方程容易,但是计算正确难.(2)中要充分运用匀强电场的特点,确定出总能量是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
16. 如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )
如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )
 如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )
如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )| A. | 微粒在电场中作匀变速曲线运动 | |
| B. | 微粒打到C点时的速率与射入电场时的速率相等 | |
| C. | MN板间的电势差为$\frac{{mv^2}_{0}}{q}$ | |
| D. | MN板间的电势差为$\frac{{Ev^2}_{0}}{2g}$ |
17. 如图所示,两个质量相等的带电粒子a、b在同一位置A以大小相同的速度射入同一匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,经磁场偏转后两粒子都经过B点,AB连线与磁场边界垂直,则( )
如图所示,两个质量相等的带电粒子a、b在同一位置A以大小相同的速度射入同一匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,经磁场偏转后两粒子都经过B点,AB连线与磁场边界垂直,则( )
 如图所示,两个质量相等的带电粒子a、b在同一位置A以大小相同的速度射入同一匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,经磁场偏转后两粒子都经过B点,AB连线与磁场边界垂直,则( )
如图所示,两个质量相等的带电粒子a、b在同一位置A以大小相同的速度射入同一匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,经磁场偏转后两粒子都经过B点,AB连线与磁场边界垂直,则( )| A. | a粒子带正电,b粒子带负电 | B. | 两粒子的轨道半径之比Ra:Rb=$\sqrt{3}$:1 | ||
| C. | 两粒子所带电荷量之比qa:qb=$\sqrt{3}$:1 | D. | 两粒子的运动时间之比ta:tb=2:$\sqrt{3}$ |
1.如图甲所示,闭合线圈固定在小车上,总质量为1kg.它们在光滑水平面上,以10m/s的速度进入与线圈平面垂直、磁感应强度为B的水平有界匀强磁场,磁场方向垂直纸面向里.已知小车运动的速度v随车的位移x变化的v-x图象如图乙所示.则( )


| A. | 线圈的长度L=15 cm | |
| B. | 磁场的宽度d=25 cm | |
| C. | 线圈进入磁场过程中做匀加速运动,加速度为0.4 m/s2 | |
| D. | 线圈通过磁场过程中产生的热量为48 J |
15.电场中有 A、B 两点,A 点的电势ϕA=-10V;,B 点的电势ϕB=10V,一个电子由 A点运动到 B 点的过程中,下列说法正确的是( )
| A. | 电场力对电子做功 20eV | B. | 电子克服电场力做功 20eV | ||
| C. | 电子的电势能增加了 20eV | D. | 电子的电势能减少了 20eV |
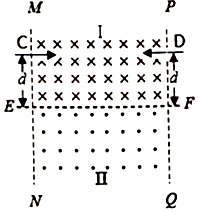 正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置,该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.
正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置,该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.
 一个初速度为零的带正电的粒子电荷量q=10-10C,质量m=10-20kg,经宽度L=8cm,电压U=200V的电场加速后,以水平速度v.穿越一宽度也为L的真空无场区域,沿中心线(图中水平虚线)飞入边长仍为L的正方形电场区域abcd,区域内有平行于ab且竖直向下的匀强电场,场强3750V/m,如图所示,若粒子飞出电场后恰好绕固定在O点的负点电荷Q开始做匀速圆周运动,不计粒子重力,不考虑各部分电场之间的相互影响(静电力常数k=9.0×109N•m2/C2),试求:
一个初速度为零的带正电的粒子电荷量q=10-10C,质量m=10-20kg,经宽度L=8cm,电压U=200V的电场加速后,以水平速度v.穿越一宽度也为L的真空无场区域,沿中心线(图中水平虚线)飞入边长仍为L的正方形电场区域abcd,区域内有平行于ab且竖直向下的匀强电场,场强3750V/m,如图所示,若粒子飞出电场后恰好绕固定在O点的负点电荷Q开始做匀速圆周运动,不计粒子重力,不考虑各部分电场之间的相互影响(静电力常数k=9.0×109N•m2/C2),试求: 如图所示,质量为m、带电量为-q的液滴从h高处自由下落,穿过A板的小孔进入匀强电场,到达B板时的速度刚好为零.设板间距离为d,不计阻力,则UAB=$\frac{mg(h+d)}{q}$,正极板是A板.(空气阻力忽略不计)
如图所示,质量为m、带电量为-q的液滴从h高处自由下落,穿过A板的小孔进入匀强电场,到达B板时的速度刚好为零.设板间距离为d,不计阻力,则UAB=$\frac{mg(h+d)}{q}$,正极板是A板.(空气阻力忽略不计)