题目内容
4.如图1所示,在2010上海世博会上,拉脱维亚馆的风洞飞行表演,令参观者大开眼界,最吸引眼球的就是正中心那个高为H=10m,直径D=4m的透明“垂直风洞”.风洞是人工产生和控制的气流,以模拟飞行器或物体周围气体的流动.在风力作用的正对面积不变时,风力F=0.06v2(v为风速).在本次风洞飞行上升表演中,表演者的质量m=60kg,为提高表演的观赏性,控制风速v与表演者上升的高度h间的关系如图2所示.g=10m/s2.求:
(1)表演者上升达最大速度时的高度h1;
(2)为防止停电停风事故,风洞备有应急电源,若在本次表演中表演者在最大高度h2时突然停电,为保证表演者的人身安全,则留给风洞自动接通应急电源滞后的最长时间tm为多长?(设接通应急电源后风洞一直以最大风速运行)
分析 (1)表演者在上升过程中当风力与重力平衡时,速度达到最大值.由图2得出v与h的关系式,代入风力F=0.06v2,得到F与h的关系,由平衡条件求出高度h1.
(2)根据F与h的关系求出表演者上升过程中风力做的功,再由动能定理求出表演者上升的最大高度h2.应急电源接通前,表演者先做自由落体运动;当应急电源接通后,做匀减速运动,恰好落到风洞底部时速度为零.根据牛顿第二定律和位移公式结合求出tm
解答 解:(1)由图2可知:v2=1.2×104-500h
即风力F=7.2×102-30h
当表演者在上升过程中的速度最大时有F=mg
代入数据得h1=4m
(2)对表演者由动能定理可得WF-mgh2=0
因WF与h成线性关系,则风力做功W${\;}_{F}=\frac{{F}_{0}+{F}_{h2}}{2}{h}_{2}$
代入数据化简得:h2=8m
当应急电源接通后,风洞以最大风速运行时滞后时间最长
表演者减速的加速度为a=$\frac{{F}_{m}-mg}{m}$=2m/s2
表演者从最高处到落地过程中有h${\;}_{2}=\frac{1}{2}g{{t}_{m}}^{2}+\frac{(g{t}_{m})^{2}}{2a}$
代入数据化简得t${\;}_{m}=\frac{2\sqrt{15}}{15}s$
答:(1)表演者上升达最大速度时的高度为4m
(2)留给风洞自动接通应急电源滞后的最长时间tm为$\frac{2\sqrt{15}}{15}$s
点评 本题根据图象写出解析式,充分利用图象的信息是本题的关键.当力与位移成线性变化时可用力的平均值与位移乘积求变化做功

 如图甲所示是一打桩机的简易模型.质量m=1kg的物块在拉力F作用下从与铁钉接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击铁钉,将铁钉打入10cm深度,物块不再被弹起.若以初始状态物块与铁钉接触处为零势能点,物块上升过程中,机械能E与上升高度h的关系图象如图乙所示.撞击前不计所有阻力,碰撞瞬间损失2J的能量,已知铁钉的质量为0.2kg,g=10m/s2.则( )
如图甲所示是一打桩机的简易模型.质量m=1kg的物块在拉力F作用下从与铁钉接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击铁钉,将铁钉打入10cm深度,物块不再被弹起.若以初始状态物块与铁钉接触处为零势能点,物块上升过程中,机械能E与上升高度h的关系图象如图乙所示.撞击前不计所有阻力,碰撞瞬间损失2J的能量,已知铁钉的质量为0.2kg,g=10m/s2.则( )| A. | 物块在F作用下向上运动的加速度为12 m/s2 | |
| B. | 物块上升过程的最大速度为2$\sqrt{6}$m/s | |
| C. | 物块上升到0.25m高度处拉力F的瞬时功率为12W | |
| D. | 铁钉被打入10cm深度的过程中受到的平均阻力为112N |
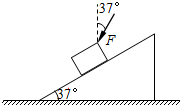 如图所示,一倾角为37°的斜劈放在水平地面上,一物体沿斜劈恰能匀速下滑.现给物体施加一个与竖直方向夹角为37°斜向下的力F=5N作用,斜劈仍静止,sin37°=0.6,cos37°=0.8.则( )
如图所示,一倾角为37°的斜劈放在水平地面上,一物体沿斜劈恰能匀速下滑.现给物体施加一个与竖直方向夹角为37°斜向下的力F=5N作用,斜劈仍静止,sin37°=0.6,cos37°=0.8.则( )| A. | 物体仍能沿斜面匀速下滑 | B. | 地面对斜劈的支持力增大4N | ||
| C. | 地面对斜劈的摩擦力大小为零 | D. | 地面对斜劈的摩擦力大小为3N |
 如图所示,在真空中有两个固定的点电荷A、B,|qA|=|qB|=q,A、B间的距离为r,图中画出了其中一根电场线,a、b、c、d位于正方形的四个顶点,其中a、c在A、B的连线上,b、d在A、B连线的中垂线上,下列说法正确的是( )
如图所示,在真空中有两个固定的点电荷A、B,|qA|=|qB|=q,A、B间的距离为r,图中画出了其中一根电场线,a、b、c、d位于正方形的四个顶点,其中a、c在A、B的连线上,b、d在A、B连线的中垂线上,下列说法正确的是( )| A. | 若B是正电荷,则b点的场强Eb>$\frac{2\sqrt{2}k{q}^{2}}{{r}^{2}}$ | |
| B. | 若a、c两点的场强大小相等,则B一定是正电荷 | |
| C. | 若Ubd=0,则A、B一定是异种电荷 | |
| D. | 若ϕa=ϕc,则B一定是负电荷 |
A.电流表A(量程0.6A,内阻约为2Ω)
B.电流表G(量程500μA,内阻Rg=200Ω)
C.守值电阻R1=29800Ω
D.定值电阻R2=9800Ω
E.滑动变阻器R3(0~100Ω,1A)
F.开关S和导线若干

(1)由于缺少电压表,结合这块电瓶标称电动势,应将电流表G和定值电阻C(填序号)串联改装成电压表,改装后的电压表量程为15V.
(2)兴趣小组根据如图1所示的电路图进行实验,记录了实验数据,并通过计算得到了6组电压U和对应电流I的值,如表所示,请你帮助他们在图2中作出U-I图象.
| 电压U/V | 9.80 | 9.30 | 8.70 | 7.80 | 7.13 | 6.42 |
| 电流I/A | 0.14 | 0.19 | 0.26 | 0.35 | 0.43 | 0.50 |
 如图所示为一简单欧姆表原理示意图,其中电流表G的满偏电流Ig=300μA,内阻Rg=100Ω,可变电阻R的最大阻值为10kΩ,电池的电动势E=1.5V,内阻r=0.5Ω,图中与接线柱A相连的表笔颜色应是红色.按正确使用方法测量电阻Rx的阻值时,指针指在刻度盘的正中央,则Rx=5 kΩ.
如图所示为一简单欧姆表原理示意图,其中电流表G的满偏电流Ig=300μA,内阻Rg=100Ω,可变电阻R的最大阻值为10kΩ,电池的电动势E=1.5V,内阻r=0.5Ω,图中与接线柱A相连的表笔颜色应是红色.按正确使用方法测量电阻Rx的阻值时,指针指在刻度盘的正中央,则Rx=5 kΩ. 在水平地面MN上方高度为h=0.45m处有一个粗糙绝缘平台PQ,如图所示,平台上方PR右侧有水平向右的有界匀强电场,场强E=1.5×103N/C.有一质量m=1.0×10-3kg、带电量为q=-1.0×10-6C的滑块放在平台上,距离平台左端P点L=1m处,滑块与平台的滑动摩擦因数为μ=0.50.现给滑块水平向左的初速度v0=4m/s,问:
在水平地面MN上方高度为h=0.45m处有一个粗糙绝缘平台PQ,如图所示,平台上方PR右侧有水平向右的有界匀强电场,场强E=1.5×103N/C.有一质量m=1.0×10-3kg、带电量为q=-1.0×10-6C的滑块放在平台上,距离平台左端P点L=1m处,滑块与平台的滑动摩擦因数为μ=0.50.现给滑块水平向左的初速度v0=4m/s,问: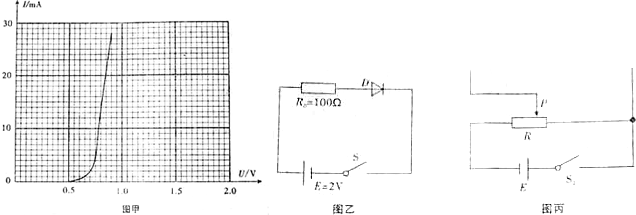
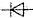 )的正向伏安特性曲线.图丙仅画出了他设计的部分电路图,请你补全完成该实验的电路图,并标明各元件的符号.
)的正向伏安特性曲线.图丙仅画出了他设计的部分电路图,请你补全完成该实验的电路图,并标明各元件的符号.