题目内容
16.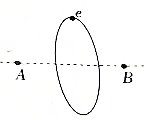 在一条水平直线上相距2a的A、B两点,固定有等量同种电荷,电荷量为q,一电子好在直线AB的中垂面上半径为a的匀速圆周运动,如图所示,已知电子的电荷量为e,重力不计,则( )
在一条水平直线上相距2a的A、B两点,固定有等量同种电荷,电荷量为q,一电子好在直线AB的中垂面上半径为a的匀速圆周运动,如图所示,已知电子的电荷量为e,重力不计,则( )| A. | A,B两点的电荷均带负电 | |
| B. | 电子轨道所在位置的场强处处相同 | |
| C. | 若将A、B两点的电荷缓慢向两侧移动,电子的轨道半径减小 | |
| D. | 电子做圆周运动的角速度为$\sqrt{\frac{\sqrt{2}kqe}{2m{a}^{3}}}$ |
分析 电子做匀速圆周运动所需要的向心力由两个点电荷库仑力的合力提供,根据库仑力的特点和力的合成,由牛顿第二定律求电子的角速度.
解答  解:A、电子做匀速圆周运动所需要的向心力由两个点电荷库仑力的合力提供,合力指向圆心O,如图,根据力的合成可知A、B处固定的点电荷对电子有引力作用,所以A,B两点的电荷均带正电.故A错误.
解:A、电子做匀速圆周运动所需要的向心力由两个点电荷库仑力的合力提供,合力指向圆心O,如图,根据力的合成可知A、B处固定的点电荷对电子有引力作用,所以A,B两点的电荷均带正电.故A错误.
B、电子轨道所在位置的场强大小处处相等,但方向不同,所以场强不同,故B错误.
C、若将A、B两点的电荷缓慢向两侧移动,它们对电子的合力减小,电子将做离心运动,轨道半径增大,故C错误.
D、根据牛顿第二定律得:2k$\frac{qe}{{a}^{2}+{a}^{2}}$cos45°=mω2a,解得ω=$\sqrt{\frac{\sqrt{2}kqe}{2m{a}^{3}}}$,故D正确.
故选:D
点评 本题有两个关键点:一是分析为库仑力的性质,确定向心力的来源;二是运用合成法求解合力.

练习册系列答案
相关题目
6. 如图所示,不带电的枕形导体 AB,帖在下面的金属箔片是闭合的,将带正电的球 C 移近枕形金属导体,下列说法中正确的是( )
如图所示,不带电的枕形导体 AB,帖在下面的金属箔片是闭合的,将带正电的球 C 移近枕形金属导体,下列说法中正确的是( )
 如图所示,不带电的枕形导体 AB,帖在下面的金属箔片是闭合的,将带正电的球 C 移近枕形金属导体,下列说法中正确的是( )
如图所示,不带电的枕形导体 AB,帖在下面的金属箔片是闭合的,将带正电的球 C 移近枕形金属导体,下列说法中正确的是( )| A. | 枕形导体中的正电荷向 B 端移动,负电荷不移动 | |
| B. | 枕形导体中电子向 A 端移动,正电荷不移动 | |
| C. | A 端金属箔片张开,B 端金属箔片闭合 | |
| D. | A 端金属箔片张开,B 端金属箔片张开 |
7.长绳的一端搁置在地球的卫星上,另一端系住升降机,放开绳,升降机能到达地球上,人坐在升降机里,科学家控制卫星上的电动机把升降机拉到卫星上.已知地球表面的重力加速度g=10m/s2,地球半径R=6400km,地球自转周期为24h,某宇航员在地球表面用体重计称得其体重为800N,站在升降机中,某时刻当升降机以加速度a=10m/s2竖直上升,这时此人再一次用同一体重计称得视重为850N,忽略地球公转及卫星受到升降机拉力对卫星运动的影响,则下列说法错误的是( )
| A. | 如果把绳的一端搁置在同步卫星上,可知绳的长度至少有多长 | |
| B. | 可以求出升降机此时距地面的高度 | |
| C. | 可以求出升降机此时所受万有引力的大小 | |
| D. | 可以求出宇航员的质量 |
1. 如图所示,在同一种均匀介质中的一条直线上,有A、B、C三点,C为AB的中点,现在A、B两点同时开始不断上下振动,A点振动的同时在B点处的观察者沿直线AB远离A点,经过一段时间后的波形如图所示,A波的波速为5m/s,以下判断正确的是( )
如图所示,在同一种均匀介质中的一条直线上,有A、B、C三点,C为AB的中点,现在A、B两点同时开始不断上下振动,A点振动的同时在B点处的观察者沿直线AB远离A点,经过一段时间后的波形如图所示,A波的波速为5m/s,以下判断正确的是( )
 如图所示,在同一种均匀介质中的一条直线上,有A、B、C三点,C为AB的中点,现在A、B两点同时开始不断上下振动,A点振动的同时在B点处的观察者沿直线AB远离A点,经过一段时间后的波形如图所示,A波的波速为5m/s,以下判断正确的是( )
如图所示,在同一种均匀介质中的一条直线上,有A、B、C三点,C为AB的中点,现在A、B两点同时开始不断上下振动,A点振动的同时在B点处的观察者沿直线AB远离A点,经过一段时间后的波形如图所示,A波的波速为5m/s,以下判断正确的是( )| A. | 观察者接收到A处产生的波的频率增加 | |
| B. | 两列波在传播过程中,若遇到大于5m的障碍物,均不能发生明显的衍射现象 | |
| C. | 中点C的振动总是加强的 | |
| D. | 能与A波发生干涉的横波的频率可以为24Hz |
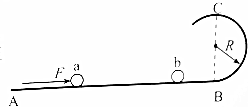 如图所示,ABC为竖直平面内的光滑轨道,AB部分水平,BC部分是半径为R的圆弧轨道.小球a、b均静止在水平轨道上,两者相隔一定距离,两小球的质量分别为ma=2m、mb=m.现对a施加一水平恒力F使其从静止开始运动,作用时间t后撤去F,之后a与b发生对心弹性正碰,要使碰后两球均能通过圆弧轨道的最高点C,求F至少应为多大?
如图所示,ABC为竖直平面内的光滑轨道,AB部分水平,BC部分是半径为R的圆弧轨道.小球a、b均静止在水平轨道上,两者相隔一定距离,两小球的质量分别为ma=2m、mb=m.现对a施加一水平恒力F使其从静止开始运动,作用时间t后撤去F,之后a与b发生对心弹性正碰,要使碰后两球均能通过圆弧轨道的最高点C,求F至少应为多大?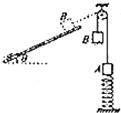 如图所示,劲度系数为k的轻弹簧下端周定在水平地面上,上端连接一质量为m的物体A,一不可伸长的轻绳跨过滑轮,两端分别与物体A及质量为2m的物体B连接,不计空气阻力、定滑轮与轻绳间的摩擦,重力加速度为g.弹簧的形变始终在弹性限度内.
如图所示,劲度系数为k的轻弹簧下端周定在水平地面上,上端连接一质量为m的物体A,一不可伸长的轻绳跨过滑轮,两端分别与物体A及质量为2m的物体B连接,不计空气阻力、定滑轮与轻绳间的摩擦,重力加速度为g.弹簧的形变始终在弹性限度内.