题目内容
16. 如图所示,一个小球从倾角为θ的光滑斜面底端O以一定速度冲上斜面.已知小球两次经过一个较低点A的时间间隔为TA,两次经过较高点B的时间间隔为TB,重力加速度为g,则A、B两点间的距离为( )
如图所示,一个小球从倾角为θ的光滑斜面底端O以一定速度冲上斜面.已知小球两次经过一个较低点A的时间间隔为TA,两次经过较高点B的时间间隔为TB,重力加速度为g,则A、B两点间的距离为( )| A. | $\frac{({T}_{A}-{T}_{B})gcosθ}{2}$ | B. | $\frac{({{T}_{A}}^{2}-{{T}_{B}}^{2})gsinθ}{4}$ | ||
| C. | $\frac{({{T}_{A}}^{2}-{{T}_{B}}^{2})gcosθ}{4}$ | D. | $\frac{({{T}_{A}}^{2}-{{T}_{B}}^{2})gsinθ}{8}$ |
分析 根据牛顿第二定律求出小球在斜面上的加速度大小,根据小球上滑和下滑的对称性得出从最高点到A点的时间和最高点到B的时间,结合位移时间公式求出A、B两点间的距离.
解答 解:根据牛顿第二定律得,小球的加速度a=$\frac{mgsinθ}{m}=gsinθ$,
小球两次经过一个较低点A的时间间隔为TA,根据对称性知,在最高点返回到A点的时间${t}_{1}=\frac{{T}_{A}}{2}$,在最高点返回到B点的时间${t}_{2}=\frac{{T}_{B}}{2}$,
则A、B两点间的距离$△x=\frac{1}{2}a{{t}_{1}}^{2}-\frac{1}{2}a{{t}_{2}}^{2}$=$\frac{1}{2}gsinθ(\frac{{{T}_{A}}^{2}}{4}-\frac{{{T}_{B}}^{2}}{4})$=$\frac{({{T}_{A}}^{2}-{{T}_{B}}^{2})gsinθ}{8}$.
故选:D.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,本题采用运动的对称性,结合位移公式进行求解比较简捷.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
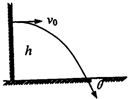
2.如图所示,在某一高处水平抛出一个物体,落地时物体速度与水平面间的夹角为θ,则( )

| A. | 抛出点高度越高,初速度越大,θ值就越大 | |
| B. | 抛出点高度越高,初速度越小,θ值就越大 | |
| C. | 抛出点高度越低,初速度越大,θ值就越大 | |
| D. | 抛出点高度越低,初速度越小,θ值就越大 |
4.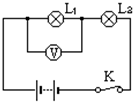 如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )
如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )
 如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )
如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )| A. | L1处短路 | B. | L2处短路 | C. | L1灯丝断了 | D. | L2灯丝断了 |
 质量为m的物体在与水平方向成α角的斜向上的拉力F的作用下,沿水平面匀速运动,如图所示.求物体与接触面间的动摩擦因数.
质量为m的物体在与水平方向成α角的斜向上的拉力F的作用下,沿水平面匀速运动,如图所示.求物体与接触面间的动摩擦因数. 如图所示,倾角为α的光滑斜面体上有一个小球被平行于斜面的细绳系于斜面上,斜面体放在水平面上.已知斜面体和小球组成的装置可沿水平方向向左或向右做直线运动.重力加速度为g,求:
如图所示,倾角为α的光滑斜面体上有一个小球被平行于斜面的细绳系于斜面上,斜面体放在水平面上.已知斜面体和小球组成的装置可沿水平方向向左或向右做直线运动.重力加速度为g,求: