题目内容
7.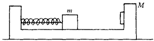 如图所示,质量为M的框架放在光滑的水平桌面上,质量为m的木块压缩着框架左侧的弹簧并用细线固定,木块距框架右侧为d.现在把线剪断,木块被弹簧推动,木块达到框架右侧并不弹回,木块与框架间的摩擦可以忽略不计.最后框架的位移为$\frac{md}{M+m}$.
如图所示,质量为M的框架放在光滑的水平桌面上,质量为m的木块压缩着框架左侧的弹簧并用细线固定,木块距框架右侧为d.现在把线剪断,木块被弹簧推动,木块达到框架右侧并不弹回,木块与框架间的摩擦可以忽略不计.最后框架的位移为$\frac{md}{M+m}$.
分析 木块与框架系统动量守恒,应用动量守恒定律可以求出框架的位移.
解答 解:木块与框架组成的系统动量守恒,由于系统初动量为零,由动量守恒定律可知,木块与框架碰撞后系统总动量为零,即两者都静止;
以向右为正方向,从剪断细线到木块与框架碰撞过程中,由动量守恒定律得:mv-Mv′=0,m$\frac{d-x}{t}$-M$\frac{x}{t}$=0,
解得:x=$\frac{md}{M+m}$;
故答案为:$\frac{md}{M+m}$.
点评 本题考查了求框架的位移,分析清楚物体运动过程,应用动量守恒定律即可正确解题.

练习册系列答案
相关题目
18.“探究加速度与物体质量、物体受力的关系”的实验中,使用电火花计时器(所用交流电的频率为50Hz),在平衡小车与木板之间摩擦力后,小车在钩码的拉力作用下做匀加速直线运动,得到如图所示的纸带.图中的点为计数点,相邻两计数点间还有三个点未画出来,相邻两计数点间的距离分别为s1、s2、s3、s4、s5和s6.下列表述正确的是 ( )


| A. | 实验时应先放开纸带再接通电源 | |
| B. | (S6一S1)等于(S2一S1)的6倍 | |
| C. | 从纸带可求出小车在拉力作用下的加速度 | |
| D. | 相邻两个计数点间的时间间隔为0.02s |
15.船和人的总质量为M,原来静止在水面上,质量为m的人从船头水平跳出后,船获得的反冲速度为V,则人跳出去时的速度为( )
| A. | $\frac{MV}{m}$ | B. | $\frac{(m-M)V}{m}$ | C. | $\frac{MV}{M-m}$ | D. | $\frac{mV}{(M+m)}$ |
2.下列说法正确的是( )
| A. | 光是一种电磁波 | B. | 光是一种概率波 | ||
| C. | 光子相当于高速运动的质点 | D. | 光的直线传播只是宏观近似规律 |
12.在光滑水平面上放一测力计,甲、乙两人分别用100N的两个力沿水平方向拉测力计的两端(测力计始终保持静止),则测力计的读数应为( )
| A. | 0 | B. | 100 N | C. | 200 N | D. | 400 N |
19.滑板以某一初速度在水平冰面上滑行一段距离后停下,以下说法正确的是( )
| A. | 前冲力对滑板做正功,摩擦力对滑板做负功 | |
| B. | 重力对滑板做正功,支持力对滑板做负功 | |
| C. | 重力对滑板做负功,支持力对滑板做正功 | |
| D. | 摩擦力对滑板做负功,重力和支持力都不做功 |
16. 质量为m,电量为q的点电荷只受电场力作用沿圆弧MN做匀速圆周运动,若圆弧MN的弧长为s,经过圆弧M、N两点的时间为t,经过这两点的速度偏向角为θ,不考虑点电荷对周围电场的影响,则( )
质量为m,电量为q的点电荷只受电场力作用沿圆弧MN做匀速圆周运动,若圆弧MN的弧长为s,经过圆弧M、N两点的时间为t,经过这两点的速度偏向角为θ,不考虑点电荷对周围电场的影响,则( )
 质量为m,电量为q的点电荷只受电场力作用沿圆弧MN做匀速圆周运动,若圆弧MN的弧长为s,经过圆弧M、N两点的时间为t,经过这两点的速度偏向角为θ,不考虑点电荷对周围电场的影响,则( )
质量为m,电量为q的点电荷只受电场力作用沿圆弧MN做匀速圆周运动,若圆弧MN的弧长为s,经过圆弧M、N两点的时间为t,经过这两点的速度偏向角为θ,不考虑点电荷对周围电场的影响,则( )| A. | M、N两点的电势相等 | |
| B. | 点电荷q的加速度大小为a=$\frac{s}{θ{t}^{2}}$ | |
| C. | 该点电荷q所处的电场可能是两个等量同种点电荷所产生的 | |
| D. | 该电场的场强方向一定指向圆弧的圆心 |
17.下列单位中与磁感应强度B的单位T相当的是( )
| A. | Wb/m2 | B. | N/A•m | C. | N/C•m | D. | V•s/m2 |
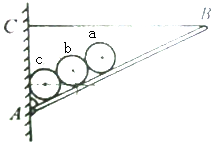 有一轻质木板AB长为L,A端用铰链固定在竖直墙上,另一端用水平轻绳CB拉住.板上依次放着a、b、c三个圆柱体,半径均为r,重均为G,木板与墙的夹角为θ,如图所示,不计一切摩擦,求BC绳上的张力.
有一轻质木板AB长为L,A端用铰链固定在竖直墙上,另一端用水平轻绳CB拉住.板上依次放着a、b、c三个圆柱体,半径均为r,重均为G,木板与墙的夹角为θ,如图所示,不计一切摩擦,求BC绳上的张力.