题目内容
5.天文工作者观测到某行星的半径为R1,自转周期为T1,它有一颗卫星,轨道半径为R2,绕行星公转周期为T2,若万有引力常量为G,求:(1)该行星的质量和平均密度;
(2)要在此行星的赤道上发射一颗近地人造卫星,使其轨道平面与行星的赤道平面重合,且设行星上无气体阻力,求该卫星相对于地心的速度是多少?
(3)该行星表面的重力加速度.
分析 (1)根据万有引力提供卫星圆周运动的向心力可以列式求出行星的质量M,进一步求密度.
(2)发射近地人造卫星的速度即为第一宇宙速度,根据万有引力提供向心力计算即可.
(3)根据重力等于万有引力,列式求得行星的地表重力加速度.
解答 解:(1)据万有引力提供卫星圆周运动的向心力,有$G\frac{Mm}{{{R}_{2}}^{2}}=m\frac{4{π}^{2}}{{{T}_{2}}^{2}}{R}_{2}$
得到 $M=\frac{4{π}^{2}{{R}_{2}}^{3}}{G{{T}_{2}}^{2}}$
又$M=ρ\frac{4}{3}π{{R}_{1}}^{3}$,
所以行星的密度 $ρ=\frac{3π{{R}_{2}}^{3}}{G{{T}_{2}}^{2}{{R}_{1}}^{3}}$
(2)根据万有引力提供向心力$G\frac{Mm}{{{R}_{1}}^{2}}=m\frac{{v}^{2}}{{R}_{1}}$,得$v=\sqrt{\frac{GM}{{R}_{1}}}$=$\sqrt{\frac{4{π}^{2}{{R}_{2}}^{3}}{{R}_{1}{{T}_{2}}^{2}}}$=$\frac{2π{R}_{2}}{{T}_{2}}\sqrt{\frac{{R}_{2}}{{R}_{1}}}$
(3)在行星的地表,有 $G\frac{Mm}{{{R}_{1}}^{2}}=mg$,
得$g=\frac{4{π}^{2}{{R}_{2}}^{3}}{{{R}_{1}}^{2}{{T}_{2}}^{2}}$
答:(1)该行星的质量为$\frac{4{π}^{2}{{R}_{2}}^{3}}{G{{T}_{2}}^{2}}$,平均密度为$\frac{3π{{R}_{2}}^{3}}{G{{T}_{2}}^{2}{{R}_{1}}^{3}}$;
(2)要在此行星的赤道上发射一颗近地人造卫星,使其轨道平面与行星的赤道平面重合,且设行星上无气体阻力,则该卫星相对于地心的速度是$\frac{2π{R}_{2}}{{T}_{2}}\sqrt{\frac{{R}_{2}}{{R}_{1}}}$.
(3)该行星表面的重力加速度为$\frac{4{π}^{2}{{R}_{2}}^{3}}{{{R}_{1}}^{2}{{T}_{2}}^{2}}$.
点评 解决问题的关键根据万有引力提供圆周运动的向心力,及万有引力等于重力,理清解题思路,难度不大.

 如图所示,在一个大氢气球下面连接着一根足够长的轻绳,一质量m1=45kg的人抓着绳子上端,此时人和气球刚好处于静止,人(可以把人看成质点)离地面的高度h=3m,已知氢气球的总质量m2=15kg,如果这个人开始沿绳向下滑,那么,能使他滑到地面的绳长至少是( )
如图所示,在一个大氢气球下面连接着一根足够长的轻绳,一质量m1=45kg的人抓着绳子上端,此时人和气球刚好处于静止,人(可以把人看成质点)离地面的高度h=3m,已知氢气球的总质量m2=15kg,如果这个人开始沿绳向下滑,那么,能使他滑到地面的绳长至少是( )| A. | 3m | B. | 9m | C. | 12m | D. | 15m |
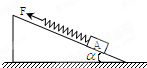 如图,倾角为α的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态.在这一过程中( )
如图,倾角为α的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态.在这一过程中( )| A. | 弹簧的伸长量为 $\frac{F-mgsinα}{k}$ | |
| B. | 弹簧的伸长量为 $\frac{mgsinα}{k}$ | |
| C. | 斜面体受地面的支持力大小等于(m+M)g | |
| D. | 斜面体受地面的静摩擦力大小等于Fcosα |
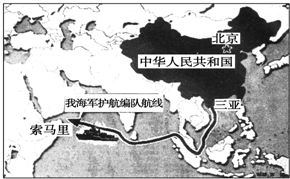 2009年1月,中国海军护航舰艇编队用时10天抵达亚丁湾索马里海域为中国商船护航.如图所示,此次护航从三亚启航,经南海、马六甲海峡,穿越印度洋,总航程四千五百海里.关于此次护航,下列说法正确的是( )
2009年1月,中国海军护航舰艇编队用时10天抵达亚丁湾索马里海域为中国商船护航.如图所示,此次护航从三亚启航,经南海、马六甲海峡,穿越印度洋,总航程四千五百海里.关于此次护航,下列说法正确的是( )| A. | 当研究护航舰艇的运行轨迹时,不能将其看做质点 | |
| B. | “四千五百海里”指的是护航舰艇的航行位移 | |
| C. | “四千五百海里”指的是护航舰艇的航行路程 | |
| D. | 根据题中数据我们可以求得此次航行的平均速度 |
| A. | 热力学第二定律揭示了大量分子参与的宏观过程的方向性 | |
| B. | 热力学第二定律有两种表述,它们是等价的 | |
| C. | 热力学第二定律包含于热力学第一定律之中 | |
| D. | 根据热力学第二定律,第二类永动机不可能制成 |
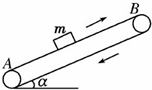 如图所示,白色的传送带两轮A、B的距离L=15m,传送带以恒定速度v=2m/s顺时针运动,现将一质量为m的小煤块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,设小煤块在运动过程中的质量不变,传送带的倾角为θ=370,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,白色的传送带两轮A、B的距离L=15m,传送带以恒定速度v=2m/s顺时针运动,现将一质量为m的小煤块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,设小煤块在运动过程中的质量不变,传送带的倾角为θ=370,g取10m/s2,sin37°=0.6,cos37°=0.8,求: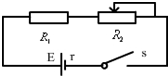 如图所示,已知电源电动势E=6V,内电阻r=2Ω,定值电阻R1=1Ω,滑动变阻器R2的最大值R2max=10Ω,求:
如图所示,已知电源电动势E=6V,内电阻r=2Ω,定值电阻R1=1Ω,滑动变阻器R2的最大值R2max=10Ω,求: 在“探究小车速度随时间变化规律”的实验中:
在“探究小车速度随时间变化规律”的实验中: 如图为某汽车直线运动的速度时间图象.从图象可知,0-2s加速度大小为3m/s2;前6秒通过的总位移为24 m.
如图为某汽车直线运动的速度时间图象.从图象可知,0-2s加速度大小为3m/s2;前6秒通过的总位移为24 m.