题目内容
12. 如图所示,斜面体固定在水平地面上,斜面光滑,倾角为θ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个小物块.木板和小物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力,大小为kmgsinθ(k>1),断开轻绳,木板和小物块一起沿斜面下滑.假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计.求:
如图所示,斜面体固定在水平地面上,斜面光滑,倾角为θ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个小物块.木板和小物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力,大小为kmgsinθ(k>1),断开轻绳,木板和小物块一起沿斜面下滑.假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计.求:(1)木板第一次与挡板碰撞后,沿斜面上升的过程中,小物块的加速度;
(2)从断开轻绳到木板与挡板第二次碰撞的过程中,木板运动的路程s;
(3)木板与挡板第二次碰撞时的速度.
分析 (1)木板上升时,对物块受力分析,在沿斜面方向上由牛顿运动定律列式求解,便可求出物块的加速度.
(2)此题要分段进行计算,第一段是木板开始下落直至第一次与挡板碰撞的过程,由几何关系可求出此过程的路程为$\frac{H}{sinθ}$,第二段是从第一次与挡板碰撞到第一次运动到最高点,第三段是从最高点下落到第二次与挡板碰撞,后两段路程相同.可由牛顿运动定律和运动学公式求得.
(3)先求出二者相对静止时的速度和位移,再根据速度和位移关系求出木板与挡板第二次碰撞时的速度
解答 解:(1)设木板第一次上升过程中,物块的加速度为a物块
物块受合力 F物块=kmgsinθ-mgsinθ
由牛顿第二定律 F物块=ma物块
联立解得 a物块=(k-1)gsinθ,
方向沿斜面向上
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1
由机械能守恒得:
$\frac{1}{2}$×2mv12=2mgH
解得:v1=$\sqrt{2gH}$
设木板弹起后的加速度a板 由牛顿第二定律 a板=-(k+1)gsinθ
木板第一次弹起的最大路程S1=$\frac{-{v}_{1}^{2}}{2{a}_{板}}$
解得
S1=$\frac{H}{(k+1)sinθ}$
木板运动的路程 S=$\frac{H}{sinθ}$+2S1$\frac{(k+3)H}{(k+1)sinθ}$
(3)设经时间t'木板与物块速度相同
则有v0-(k-1)gsinθt′=-v0+(k+1)gsinθt'
解得:t'=$\frac{{v}_{0}}{kgsinθ}$
这时物块的速度v'=v0-(k-1)gsinθt'=$\frac{{v}_{0}}{k}$
这过程中木板的位移
x=$\frac{v{′}^{2}-{v}_{0}^{2}}{-2(k+1)gsinθ}$=$\frac{{v}_{0}^{2}(k-1)}{2gsinθ{k}^{2}}$
根据位移和速度关系可得:
v22-v'2=2gsinθx
解得木板与挡板第二次碰撞时的速度为v2=$\frac{{v}_{0}}{k}$=$\sqrt{\frac{2gH}{k}}$
答:(1)木板第一次与挡板碰撞后,沿斜面上升的过程中,小物块的加速度为(k-1)gsinθ,
(2)从断开轻绳到木板与挡板第二次碰撞的过程中,木板运动的路程s为$\frac{H}{sinθ}$+2S1$\frac{(k+3)H}{(k+1)sinθ}$;
(3)木板与挡板第二次碰撞时的速度为$\sqrt{\frac{2gH}{k}}$
点评 本题综合考查了动能定理、牛顿第二定律以及共点力平衡条件的应用,要注意正确分析物理过程,正确受力分析,再正确选择物理规律求解即可.

 利用如图所示的试验装置可以测量磁场的磁感应强度的大小;用绝缘轻质细线把底边长为L、电阻为R、质量为m的U形线框竖直悬挂在力敏传感器的挂钩上,将线框置于待测磁场中(可视为匀强磁场),线框平面与磁场方向垂直,用轻质导线在连接线框与直流电源,电源电阻不计,电动势可调,导线的电阻忽略不计;当外界拉力F作用于力敏传感器的挂钩上时,力敏传感器会显示拉力的大小为F;当线框接电动势为E1时,力敏传感器显示拉力的大小为F1; 当线框接电动势为E2时,力敏传感器显示拉力的大小为F2;下列说法正确的是( )
利用如图所示的试验装置可以测量磁场的磁感应强度的大小;用绝缘轻质细线把底边长为L、电阻为R、质量为m的U形线框竖直悬挂在力敏传感器的挂钩上,将线框置于待测磁场中(可视为匀强磁场),线框平面与磁场方向垂直,用轻质导线在连接线框与直流电源,电源电阻不计,电动势可调,导线的电阻忽略不计;当外界拉力F作用于力敏传感器的挂钩上时,力敏传感器会显示拉力的大小为F;当线框接电动势为E1时,力敏传感器显示拉力的大小为F1; 当线框接电动势为E2时,力敏传感器显示拉力的大小为F2;下列说法正确的是( )| A. | 当线框接电动势为E1的电源时所受安培力的大小为F1 | |
| B. | 当线框接电动势为E2的电源时力敏传感器显示的拉力大小为线框所受安培力大小与重力大小之差 | |
| C. | 待测磁场的磁感应强度为$\frac{({F}_{1}-{F}_{2})R}{({E}_{2}-{E}_{1}^{\;})L}$ | |
| D. | 待测磁场的磁感应强度为$\frac{({F}_{1}-{F}_{2})R}{({E}_{1}-{E}_{2})L}$ |
 乐乐同学想利用“电磁弹簧秤”称量一金属棒的质量,如图所示,一根粗细均匀的金属棒ab用两个完全相同的弹簧悬挂在匀强磁场中,碰场的磁感应强度方向垂直于纸面向里,弹簧上端固定,下端与金属棒连接且绝缘,金属棒通过开关与一电路相连,电源右侧为正极,开关接通以后,下列说法正确的是( )
乐乐同学想利用“电磁弹簧秤”称量一金属棒的质量,如图所示,一根粗细均匀的金属棒ab用两个完全相同的弹簧悬挂在匀强磁场中,碰场的磁感应强度方向垂直于纸面向里,弹簧上端固定,下端与金属棒连接且绝缘,金属棒通过开关与一电路相连,电源右侧为正极,开关接通以后,下列说法正确的是( )| A. | 金属棒所受安培力竖直向下 | |
| B. | 仅改变电流方向,安培力方向不变 | |
| C. | 仅增大磁感应强度,安培力变小 | |
| D. | 若滑动变阻器的滑片向左滑动,则安培力减小 |
 如图所示是A、B两质点从同一地点运动的x-t图象,A质点的图象为直线,B质点的图象为曲线,两图象在t=4s时相交,则下列说法正确的是( )
如图所示是A、B两质点从同一地点运动的x-t图象,A质点的图象为直线,B质点的图象为曲线,两图象在t=4s时相交,则下列说法正确的是( )| A. | A质点做匀加速直线运动 | |
| B. | B质点在前4s做减速运动,4s后做加速运动 | |
| C. | 在0~4s内,质点B的通过的路程大于80m | |
| D. | A、B两质点在4s末相遇 |
 如图所示两个等量异种的点电荷在其连线的中垂线上有与连线中点O等距离的两点,a、b,在连线上有距中点O等距离的两点c、d,分别用Ea、Eb、Ec、Ed、EO,φa、φb、φc、φd、φO表示个点的场强和电势,则下列说法正确的是( )
如图所示两个等量异种的点电荷在其连线的中垂线上有与连线中点O等距离的两点,a、b,在连线上有距中点O等距离的两点c、d,分别用Ea、Eb、Ec、Ed、EO,φa、φb、φc、φd、φO表示个点的场强和电势,则下列说法正确的是( )| A. | Ea=Eb<EO,Ec=Ed>EO | |
| B. | φa=φb=φO,φc>φO>φd | |
| C. | 将一个正点电荷从a点释放,只在电场力作用下它将沿直线加速运动到b | |
| D. | 将一个正点电荷从c点释放,只在电场力作用下它将沿直线加速运动到d |
| A. | 所有材料的电阻率都随温度的升高而增大 | |
| B. | 用来制作标准电阻的材料的电阻率几乎不随温度的变化而变化 | |
| C. | 电阻率由导体材料和温度决定 | |
| D. | 电阻率ρ与导体的长度和横截面积有关 |

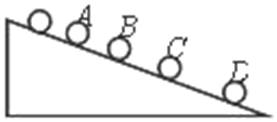 从斜面上某位置,每隔0.1s由静止开始释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB=15cm,sBC=20cm,试求:
从斜面上某位置,每隔0.1s由静止开始释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB=15cm,sBC=20cm,试求: “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.