题目内容
18．在平直轨道上，乙在甲前面，两物体相距为s，同向同时开始运动，甲以初速度v1、加速度为a1做匀加速运动，乙以初速度为零、加速度为a2做匀加速运动．假定甲能从乙旁边通过而互不影响，下列情况可能发生的是（ ）| A． | 当a1=a2时，甲、乙相遇两次 | B． | 当a1＞a2时，甲、乙相遇两次 | ||
| C． | 当a1＞a2时，甲、乙相遇一次 | D． | 当a1＜a2时，甲、乙相遇两次 |
分析 甲、乙均做匀加速直线运动，则从二者第一次相遇开始，分析以后二者能否再次位置相同，则可分析能否再次相遇．
解答 解：A、甲从乙的旁边通过说明相遇时甲的速度大于乙的速度，若a1=a2，则以后甲的速度将都大于乙的速度，故不会再次相遇，故A错误，
B、C、若a1＞a2，则甲经过乙的旁边以后，甲的速度增加更快，故甲将一直在乙的前面，故B错误，C正确；
D、若a1＜a2，则此后某一时刻乙的速度一定会大于甲的速度，故乙将会追上甲，甲乙将再次相遇，故能相遇两次，故D正确
故选：CD
点评 本题为追及相遇问题，首先要从题意中找中运动的情景，再由运动学中位移关系确定二者能否再次相遇；本题也可由图象进行分析．
练习册系列答案
全能测控期末小状元系列答案
相关题目
8．
如图所示，斜面上有a、b、c、d 四个点，ab=bc=cd，从a点以初动能E0水平抛出一个小球，它落在斜面上的b点，若小球从 a 点以初动能 2E0水平抛出，不计空气阻力，则下列判断正确的是（ ）
如图所示，斜面上有a、b、c、d 四个点，ab=bc=cd，从a点以初动能E0水平抛出一个小球，它落在斜面上的b点，若小球从 a 点以初动能 2E0水平抛出，不计空气阻力，则下列判断正确的是（ ）| A． | 小球一定落在c点与d点之间 | |
| B． | 小球一定落在c点 | |
| C． | 小球落在斜面的运动方向与斜面的夹角一定相同 | |
| D． | 小球落在斜面的运动方向与斜面的夹角一定增大 |
6．
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入粗糙水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒通过速度传感器测量物体的瞬时速度大小，下表给出了部分测量数据．求：
（1）物体在斜面加速度a1大小和水平面上的加速度a2大小；
（2）从A点达到C点的时间t；
（3）到达B点的瞬时速度vB大小；
（4）t=0.6s时瞬时速度大小v．
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入粗糙水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒通过速度传感器测量物体的瞬时速度大小，下表给出了部分测量数据．求：| t/（s） | 0.0 | 0.2 | 0.4 | … | 1.4 | 1.6 | … |
| v/（m/s） | 0.0 | 1.2 | 2.4 | … | 0.8 | 0.4 | … |
（2）从A点达到C点的时间t；
（3）到达B点的瞬时速度vB大小；
（4）t=0.6s时瞬时速度大小v．
4．一质点从O点由静止出发做匀加速直线运动，途经A、B、C三点和D、E、F三点，AB间距离为S1，BC间距离为S2，且过AB和BC段时间相等；而DE段和EF段距离相等，过DE段的平均速度为v1，过EF段的平均速度为v2．则OA间距离和过E点的速率分别为（ ）
| A． | $\frac{（3{S}_{1}-{S}_{2}）^{2}}{8（{S}_{2}-{S}_{1}）}$；$\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{{v}_{2}-{v}_{1}}$ | |
| B． | $\frac{（3{S}_{1}-{S}_{2}）^{2}}{8（{S}_{2}-{S}_{1}）}$；$\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{{v}_{1}+{v}_{2}}$ | |
| C． | $\frac{（3{S}_{1}-{S}_{2}）^{2}}{8（{S}_{2}+{S}_{1}）}$；$\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{{v}_{2}-{v}_{1}}$ | |
| D． | $\frac{（3{S}_{1}+{S}_{2}）^{2}}{8（{S}_{2}-{S}_{1}）}$；$\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{{v}_{1}+{v}_{2}}$ |
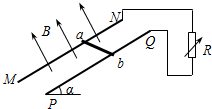如图所示，光滑且足够长平行金属导轨MN．PQ相距L=1m，导轨平面与水平面夹角α=30°，导轨电阻不计．磁感应强度B=2T的匀强磁场垂直导轨平面斜向上，一金属棒ab垂直于MN．PQ放置在导轨上，且始终与导轨接触良好，金属棒质量m=0.8kg，电阻r=2Ω．两金属导轨的上端连接一电阻箱R，调节电阻箱使R=8Ω，现
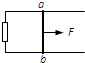如图所示，位于水平面内的两根平行的光滑金属导轨处在匀强磁场中，磁场方向垂直于导轨所在的平面，导轨的一端与一电阻相连，金属杆ab放在导轨上并与导轨垂直，现用以平行于导轨的恒力F拉ab，使之由静止开始向右运动．金属杆ab和导轨的电阻不计，用E表示回路中的感应电动势，i表示回路中的感应电流，在i随时间增大的过程中，电阻消耗的瞬时功率（ ）
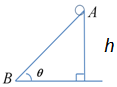如图所示，空间内有平行于纸面的匀强电场，该电场中有一个倾角θ=53o的光滑斜面．一个质量为2kg的小球在斜面上的A点保持静止，该小球的带电量Q=+4C，A点到地面的竖直高度h=25m（g=10m/s2）