题目内容
9.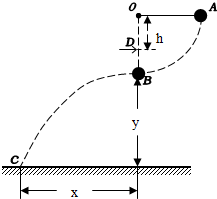 质量为m=0.5kg的小球用长为?的细线悬挂于O点,在O的正下方h=1.2m的D处有一刀口向右的刀片,现把小球拉到A处,使OA呈水平状态,无初速放手后小球摆到B处,由于细线被割断,小球水平飞出,下落y=5m后刚好落到地面上,水平射程x=6m,试求
质量为m=0.5kg的小球用长为?的细线悬挂于O点,在O的正下方h=1.2m的D处有一刀口向右的刀片,现把小球拉到A处,使OA呈水平状态,无初速放手后小球摆到B处,由于细线被割断,小球水平飞出,下落y=5m后刚好落到地面上,水平射程x=6m,试求(1)小球刚飞出的速度v0?
(2)细线长L为多长?
(3)细线被刀片挡住时线细对小球的拉力F为多少?
分析 (1)小球从B点做平抛运动,根据平抛运动的特点求得抛出时的速度;
(2)从A到B根据动能定理求得绳长
(3)根据牛顿第二定律求得绳子的拉力
解答 解:(1)从B点做平抛运动,在竖直方向做自由落体运动,故
$y=\frac{1}{2}g{t}^{2}$
t=$\sqrt{\frac{2y}{g}}=\sqrt{\frac{2×5}{10}}s=1s$
抛出时的速度为v=$\frac{x}{t}=\frac{6}{1}m/s=6m/s$
(2)从A到B有动能定理可得
$mgl=\frac{1}{2}m{v}^{2}-0$
解得l=$\frac{m{v}^{2}}{2mg}=\frac{{v}^{2}}{2g}=\frac{{6}^{2}}{2×10}m=1.8m$
(3)在B点根据牛顿第二定律可得F-mg=$\frac{m{v}^{2}}{l-h}$
解得F=$mg+\frac{m{v}^{2}}{l-h}$$0.5×10+\frac{0.5×{6}^{2}}{1.8-1.2}$N=35N
答:(1)小球刚飞出的速度v0为6m/s
(2)细线长L为1.8m
(3)细线被刀片挡住时线细对小球的拉力F为35N
点评 本题主要考查了动能定理和平抛运动,关键是抓住运动过程的分析,明确物体在各个过程的运动即可

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
15.正在斜面上匀速行驶的汽车,则在运动过程中不做功的力是( )
| A. | 重力 | B. | 支持力 | C. | 牵引力 | D. | 摩擦力 |
20. 如图所示,由半径为R的$\frac{3}{4}$光滑圆周和倾角为45°的光滑斜面组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接.一小球恰能过最高点,并始终贴着轨道内侧顺时针转动.则小球通过斜面的时间为(重力加速度为g)( )
如图所示,由半径为R的$\frac{3}{4}$光滑圆周和倾角为45°的光滑斜面组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接.一小球恰能过最高点,并始终贴着轨道内侧顺时针转动.则小球通过斜面的时间为(重力加速度为g)( )
 如图所示,由半径为R的$\frac{3}{4}$光滑圆周和倾角为45°的光滑斜面组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接.一小球恰能过最高点,并始终贴着轨道内侧顺时针转动.则小球通过斜面的时间为(重力加速度为g)( )
如图所示,由半径为R的$\frac{3}{4}$光滑圆周和倾角为45°的光滑斜面组成的轨道固定在竖直平面内,斜面和圆周之间由小圆弧平滑连接.一小球恰能过最高点,并始终贴着轨道内侧顺时针转动.则小球通过斜面的时间为(重力加速度为g)( )| A. | 2$\sqrt{gR}$ | B. | 2$\sqrt{\frac{R}{g}}$ | C. | (2$\sqrt{2}$-2)$\sqrt{\frac{R}{g}}$ | D. | ($\sqrt{10}$-$\sqrt{6}$)$\sqrt{\frac{R}{g}}$ |
4.图(a)表示t=0时的简皆波的波形图.波沿x轴正方向传播,图(b)为一质点的振动曲线.则图(a)中所表示的x=0处质点振动的初相位与图(b)所表示的振动的初相位分别为( )

| A. | 均为零 | B. | 均为$\frac{π}{2}$ | C. | 均为$-\frac{π}{2}$ | D. | $\frac{π}{2}$与$-\frac{π}{2}$ | ||||
| E. | $-\frac{π}{2}$与$\frac{π}{2}$ |
14.下面的物理量中,是矢量的是( )
| A. | 长度 | B. | .摩擦力 | C. | 位移 | D. | .路程 |
18. 一质点自原点出发,沿x轴正方向以加速度a加速,经时间t0速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加速度再变为-a0,直至速度变为-$\frac{{v}_{0}}{8}$…,其v-t图象如图所示,则下列说法中正确的是( )
一质点自原点出发,沿x轴正方向以加速度a加速,经时间t0速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加速度再变为-a0,直至速度变为-$\frac{{v}_{0}}{8}$…,其v-t图象如图所示,则下列说法中正确的是( )
 一质点自原点出发,沿x轴正方向以加速度a加速,经时间t0速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加速度再变为-a0,直至速度变为-$\frac{{v}_{0}}{8}$…,其v-t图象如图所示,则下列说法中正确的是( )
一质点自原点出发,沿x轴正方向以加速度a加速,经时间t0速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加速度再变为-a0,直至速度变为-$\frac{{v}_{0}}{8}$…,其v-t图象如图所示,则下列说法中正确的是( )| A. | 质点在t0将改变运动方向 | |
| B. | 质点将在x轴上做单向直线运动 | |
| C. | 质点运动过程中离原点的最大距离为v0t0 | |
| D. | 质点在t0内运动的平均速度为$\frac{{v}_{0}}{2}$ |
19.理想变压器的原、副线圈匝数比为10:1,下列说法中正确的是( )
| A. | 穿过原、副线圈每一匝的磁通量之比是10:1 | |
| B. | 穿过原、副线圈每一匝的磁通量之比是1:10 | |
| C. | 正常工作时,原、副线圈的输入、输出电压之比为10:1 | |
| D. | 正常工作时,原、副线圈的输入、输出电压之比为1:10 |
 如图所示,虚线三角形ABC内为磁感应强度为B的匀强磁场区域,三角形ABC是等腰直角三角形,斜边AB的长度为2L,AB边位于光滑绝缘水平面内.边长bc为2L,边长ab为L的矩形形金属线框abcd,电阻为R,在拉力F的作用下,线框以恒定的速度v沿AB运动,并穿过图中所示的匀强磁场区域.规定电流顺时针方向为正方向,力F向右为正方向,从线框进入磁场开始计时,则电流I和拉力F随时间的变化图线为选项中的是图( )
如图所示,虚线三角形ABC内为磁感应强度为B的匀强磁场区域,三角形ABC是等腰直角三角形,斜边AB的长度为2L,AB边位于光滑绝缘水平面内.边长bc为2L,边长ab为L的矩形形金属线框abcd,电阻为R,在拉力F的作用下,线框以恒定的速度v沿AB运动,并穿过图中所示的匀强磁场区域.规定电流顺时针方向为正方向,力F向右为正方向,从线框进入磁场开始计时,则电流I和拉力F随时间的变化图线为选项中的是图( )


