题目内容
4.图(a)表示t=0时的简皆波的波形图.波沿x轴正方向传播,图(b)为一质点的振动曲线.则图(a)中所表示的x=0处质点振动的初相位与图(b)所表示的振动的初相位分别为( )
| A. | 均为零 | B. | 均为$\frac{π}{2}$ | C. | 均为$-\frac{π}{2}$ | D. | $\frac{π}{2}$与$-\frac{π}{2}$ | ||||
| E. | $-\frac{π}{2}$与$\frac{π}{2}$ |
分析 根据波动图象与与振动图象分别写出波动方程与振动方程,由两个方程的表达式即可正确求出.
解答 解:设该波的振幅为A,波长为λ,圆频率为ω,该波沿x轴正方向传播,则由波动方程$y=Acos(ωt+\frac{2π}{λ}•x+{φ}_{10})$
由图可知,该波x=0处的质点的波动方程为:y=Acos(ωt+φ10)=Acos(ωt+$\frac{π}{2}$)
所以:φ10=$\frac{π}{2}$
由图b,结合振动方程y=Acos(ωt+φ0)
可得该波b质点的振动方程为:$y=Acos(ωt-\frac{π}{2})$
所以:φ20=-$\frac{π}{2}$
故选:D
点评 该题考查简谐波的波动方程与振动方程,属于大学物理的内容,在高中物理竞赛中也有出现,比较少,由参加物理竞赛的同学可以供参考.

练习册系列答案
相关题目
10.关于地磁场,下列说法正确的是( )
| A. | 地磁场的N极在地球的南极附近 | |
| B. | 北京地区地磁场方向由北向南 | |
| C. | 地球周围的磁感线从地球地理南极附近出发,回到地球地理北极附近 | |
| D. | 在地磁南(S)极处,可以自由转动的小磁针的N极竖直指向地面 |
12.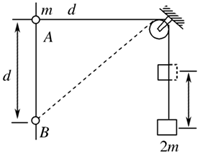 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\sqrt{2}d$ | |
| B. | 环到达B处时,环与重物的速度大小满足${v_物}=\sqrt{2}{v_环}$ | |
| C. | 环到达B,重物的速度大小${v_物}=\frac{{\sqrt{(6-4\sqrt{2})gd}}}{2}$ | |
| D. | 环从A到达B的过程中,环克服轻绳拉力做的功($\sqrt{2}$-1)mgd |
19.下列说法正确的是 ( )
| A. | 物体的温度越高,分子热运动越剧烈 | |
| B. | 液晶的光学性质不随温度、电磁作用变化而改变 | |
| C. | 只有热传递才能改变物体的内能 | |
| D. | 利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的 | |
| E. | 将一个分子从无穷远处无限靠近另一个分子,则这两个分子间的分子力先增大后减小最后再增大. |
16.两个分力,其中一个力F1为30N,另一力F2为12N,那么合力F的大小可能是( )
| A. | 10N | B. | 25N | C. | 30N | D. | 45N |
13.质量为m的物体,在距地面为h的高处,以$\frac{2g}{3}$的恒定加速度由静止竖直下落到地面,对于这一下落过程中,下列说法中正确的是( )
| A. | 物体的重力势能减少$\frac{mgh}{3}$ | B. | 物体的机械能减少$\frac{2mgh}{3}$ | ||
| C. | 物体的动能增加$\frac{2mgh}{3}$ | D. | 重力做功$\frac{2mgh}{3}$ |
14.关于弹性势能,下列说法中正确的是( )
| A. | 弹簧在任何状态下都具有弹性势能 | |
| B. | 弹簧只有在发生弹性形变时才具有弹性势能 | |
| C. | 弹性势能不可以与其他形式的能相互转化 | |
| D. | 弹性势能在国际单位中的单位是瓦特 |
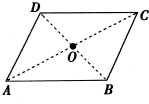 在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.
在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.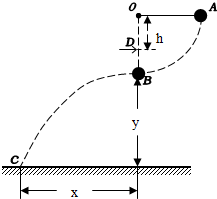 质量为m=0.5kg的小球用长为?的细线悬挂于O点,在O的正下方h=1.2m的D处有一刀口向右的刀片,现把小球拉到A处,使OA呈水平状态,无初速放手后小球摆到B处,由于细线被割断,小球水平飞出,下落y=5m后刚好落到地面上,水平射程x=6m,试求
质量为m=0.5kg的小球用长为?的细线悬挂于O点,在O的正下方h=1.2m的D处有一刀口向右的刀片,现把小球拉到A处,使OA呈水平状态,无初速放手后小球摆到B处,由于细线被割断,小球水平飞出,下落y=5m后刚好落到地面上,水平射程x=6m,试求