题目内容
20.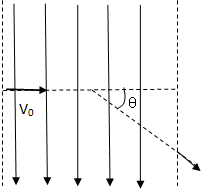 如图所示,在虚线所示的宽度范围内,存在竖直向下的电场强度为E的匀强电场,某种正离子以初速度V0垂直于左边界射入,离开右边界时的偏转角为θ,在同样宽度范围内,若只存在方向垂直纸面向外的匀强磁场,使该粒子以原来的初速度穿过该区域,偏转角扔为θ,(不计离子的重力),求:
如图所示,在虚线所示的宽度范围内,存在竖直向下的电场强度为E的匀强电场,某种正离子以初速度V0垂直于左边界射入,离开右边界时的偏转角为θ,在同样宽度范围内,若只存在方向垂直纸面向外的匀强磁场,使该粒子以原来的初速度穿过该区域,偏转角扔为θ,(不计离子的重力),求:(1)匀强磁场的磁感应强度大小
(2)离子穿过磁场和电场时间之比.
分析 (1)粒子在电场中做类平抛运动,在磁场中做匀速圆周运动,由类平抛运动规律、牛顿第二定律可以求出磁感应强度大小.
(2)求出粒子在电场与磁场中的运动时间,然后求出时间之比.
解答  解:(1)设虚线宽度为d,离子在电场中做类平抛运动,
解:(1)设虚线宽度为d,离子在电场中做类平抛运动,
竖直方向:vy=v0tanθ…①
vy=at=$\frac{qE}{m}$t…②
水平方向:d=v0t…③
当改用匀强磁场时,离子做匀速圆周运动,由牛顿第二定律得:qv0B=m$\frac{{{v}_{0}}^{2}}{r}$…④
由几何知识可知,轨道半径:r=$\frac{d}{sinθ}$…⑤
由①②③④⑤解得:B=$\frac{Ecosθ}{{v}_{0}}$;
(2)离子在电场中运动的时间为:t1=$\frac{d}{{v}_{0}}$…⑥
离子在磁场中运动的时间:t2=$\frac{rθ}{{v}_{0}}=\frac{dθ}{{v}_{0}sinθ}$…⑦
解得:$\frac{{t}_{1}}{{t}_{2}}=\frac{sinθ}{θ}$.
答:(1)匀强磁场的磁感应强度大小为$\frac{Ecosθ}{{v}_{0}}$;
(2)离子穿过电场和磁场的时间之比为$\frac{sinθ}{θ}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程、应用类平抛运动规律、牛顿第二定律、粒子在磁场中做圆周运动的周期公式即可正确解题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
5. 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )| A. | a粒子的速度比b粒子速度小 | |
| B. | a粒子在磁场中的运动时间比b粒子短 | |
| C. | 两粒子离开磁场时的速度反向延长线一定都过圆心 | |
| D. | 两粒子离开磁场时的速度反向延长线不一定都过圆心 |
10.若汽车的加速度方向与速度方向一致,当加速度减小时,则( )
| A. | 汽车的速度在减小,汽车的位移也在减小 | |
| B. | 汽车的速度在增大,汽车的位移也在增大 | |
| C. | 汽车速度在减小,当加速度减小到零时,汽车静止 | |
| D. | 当加速度减小到零时,汽车的速度达到最大 |
 如图所示,在y轴的右方有一磁感应强度为B的方向垂直纸面向外的匀强磁场,在x轴的下方有一场强为E的方向平行x轴向左的匀强电场.有一铅板放置在y轴处,且与纸面垂直.现有一质量为m、电荷量为q的粒子由静止经过加速电压为U的电场加速,然后以垂直于铅板的方向从A处沿直线穿过铅板,而后从x轴上的D处以与x轴正向夹角为60°的方向进入电场和磁场叠加的区域,最后到达y轴上的C点.已知OD长为L,不考虑粒子受到的重力,求:
如图所示,在y轴的右方有一磁感应强度为B的方向垂直纸面向外的匀强磁场,在x轴的下方有一场强为E的方向平行x轴向左的匀强电场.有一铅板放置在y轴处,且与纸面垂直.现有一质量为m、电荷量为q的粒子由静止经过加速电压为U的电场加速,然后以垂直于铅板的方向从A处沿直线穿过铅板,而后从x轴上的D处以与x轴正向夹角为60°的方向进入电场和磁场叠加的区域,最后到达y轴上的C点.已知OD长为L,不考虑粒子受到的重力,求: 如图所示,足够长的粗糙金属导轨POQ,夹角∠POQ=60°,PO=OQ,P、Q两端点均在水平面上,导轨平面与水平面的夹角为α.质量为m的匀质金属杆MN垂直于∠POQ的角平分线对称放置在导轨上,其重心在角平分线上.金属杆和导轨单位长度的电阻均为r,且始终保持良好接触.若用大小F=2mgsinα、方向沿∠POQ的角平分线向上的力F作用在金属杆MN的重心点上,金属杆恰可沿力F的方向匀速向上运动.撤去力F后,给导轨处加上一个区域足够大的磁感应强度为B的匀强磁场(图中未画出),磁场方向垂直于导轨平面.初始时刻金属杆到O点的距离为a,给金属杆一个沿∠POQ角平分线向下的初速度v0.求:(不计感应电流之间的相互作用)
如图所示,足够长的粗糙金属导轨POQ,夹角∠POQ=60°,PO=OQ,P、Q两端点均在水平面上,导轨平面与水平面的夹角为α.质量为m的匀质金属杆MN垂直于∠POQ的角平分线对称放置在导轨上,其重心在角平分线上.金属杆和导轨单位长度的电阻均为r,且始终保持良好接触.若用大小F=2mgsinα、方向沿∠POQ的角平分线向上的力F作用在金属杆MN的重心点上,金属杆恰可沿力F的方向匀速向上运动.撤去力F后,给导轨处加上一个区域足够大的磁感应强度为B的匀强磁场(图中未画出),磁场方向垂直于导轨平面.初始时刻金属杆到O点的距离为a,给金属杆一个沿∠POQ角平分线向下的初速度v0.求:(不计感应电流之间的相互作用)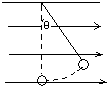 如图所示,小球的质量为m,带电量为q,悬挂小球的丝线与竖直方向成θ角时,小球恰好在匀强电场中静止不动,丝线长度为l.
如图所示,小球的质量为m,带电量为q,悬挂小球的丝线与竖直方向成θ角时,小球恰好在匀强电场中静止不动,丝线长度为l.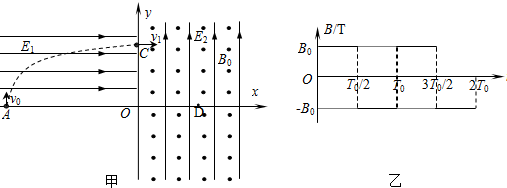 在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,场强为E1.坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=$\frac{1}{2}$E1,匀强磁场方向垂直纸面.处在第三象限的发射装置(图中未画出)竖直向上射出一个比荷$\frac{q}{m}$=102C/kg的带正电的粒子(可视为质点),该粒子以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限.取粒子刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g=10m/s2.试求:
在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,场强为E1.坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=$\frac{1}{2}$E1,匀强磁场方向垂直纸面.处在第三象限的发射装置(图中未画出)竖直向上射出一个比荷$\frac{q}{m}$=102C/kg的带正电的粒子(可视为质点),该粒子以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限.取粒子刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g=10m/s2.试求: 如图所示,真空室内有一个点状的α粒子放射源P,它向各个方向发射α粒子(不计重力),速率都相同,ab为P点附近的一条水平直线(P到直线ab的距离PC=L),Q为直线ab上一点,它与P点相距PQ=$\frac{\sqrt{5}}{2}$L(现只研究与放射源P和直线ab同一平面内的α粒子的运动),当真空室内(直线ab以上区域)只存在垂直该平面向里、磁感应强度为B的匀强磁场时,不同方向发射的α粒子若能到达ab直线,则到达ab直线时它们动能都相等,已知水平向左射出的α粒子也恰好到达Q点.(α粒子的电荷量为+q,质量为m,sin37°=0.6,cos37°=0.8)求:
如图所示,真空室内有一个点状的α粒子放射源P,它向各个方向发射α粒子(不计重力),速率都相同,ab为P点附近的一条水平直线(P到直线ab的距离PC=L),Q为直线ab上一点,它与P点相距PQ=$\frac{\sqrt{5}}{2}$L(现只研究与放射源P和直线ab同一平面内的α粒子的运动),当真空室内(直线ab以上区域)只存在垂直该平面向里、磁感应强度为B的匀强磁场时,不同方向发射的α粒子若能到达ab直线,则到达ab直线时它们动能都相等,已知水平向左射出的α粒子也恰好到达Q点.(α粒子的电荷量为+q,质量为m,sin37°=0.6,cos37°=0.8)求: 如图所示,平行金属板长为L,一个带电为+q质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成30°角,粒子重力不计,求:
如图所示,平行金属板长为L,一个带电为+q质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成30°角,粒子重力不计,求: