题目内容
12．某同学要测量一均匀新材料制成的圆柱体的电阻率ρ．步骤如下：
（1）用游标为20分度的卡尺测量其长度如图1，由图可知其长度L=50.15mm；
（2）用螺旋测微器测量其直径如图2，由图可知其直径D=4.699mm；
（3）用多用电表的电阻“×10”挡，按正确的操作步骤测此圆柱体的电阻，表盘的示数如图3，则该电阻的阻值R=300Ω．
（4）该同学想用伏安法更精确地测量其电阻R，现有的器材及其代号和规格如下：
待测圆柱体电阻R
电流表A1（量程0～10mA，内阻约50Ω）
电流表A2（量程0～50mA，内阻约30Ω）
电压表V1（量程0～3V，内阻约30kΩ）
电压表V2（量程0～15V，内阻约50kΩ）
直流电源E（电动势4V，内阻不计）
滑动变阻器R1（阻值范围0～50Ω，允许通过的最大电流0.5A）
开关S、导线若干．
为使实验误差较小，要求测得多组数据进行分析，请在图4中画出测量的电路图，并标明所用器材的代号．
分析 题（1）游标卡尺读数时应分成整数部分和小数部分两部分来读，注意分度大小；题（2）螺旋测微器读数时应分成整数部分和小数部分两部分来读，注意半毫米刻度线是否露出；题（4）首先根据电源电动势大小选择出电压表的量程，再通过求出通过待测电阻的最大电流来选择电流表量程，根据电流表内外接法的选择方法判定应采用内接法；根据要求多测几组数据可知变阻器应采用分压式接法，即电路应是分压外接电路．
解答 解；（1）游标卡尺的读数为：L=50mm+3×0.05mm=50.15mm；
（2）螺旋测微器的读数为：D=4.5mm+19.9×0.01mm=4.699（4.700±0.001）；
（3）欧姆表的读数为：R=30×10Ω=300Ω；
（4）根据电源的电动势为4V可知电压表应选择${V}_{1}^{\;}$；
由于通过待测电阻的最大电流为${I}_{max}^{\;}$=$\frac{E}{{R}_{x}^{\;}}$=$\frac{4}{300}A$=13mA，所以电流表应选择${A}_{1}^{\;}$；
由于待测电阻满足$\frac{{R}_{V}^{\;}}{{R}_{x}^{\;}}$$＞\frac{{R}_{x}^{\;}}{{R}_{A}^{\;}}$，所以电流表应用外接法；
由于实验要求能测多组数据，所以变阻器应采用分压式接法，电路图如图所示：
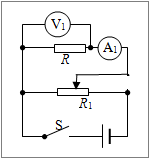
故答案为：（1）50.15；（2）4.699；（3）300；（4）如图
点评 应明确：①游标卡尺和螺旋测微器读数时应分成整数部分和小数部分两部分来读；②根据电源电动势大小来选择电压表的量程，根据通过待测电阻的最大电流来选择电流表的量程，若实验要求多测几组数据或要求电压从零调或不正确的全电阻远小于待测电阻时，变阻器应采用分压式接法；③当待测电阻满足$\frac{{R}_{V}^{\;}}{{R}_{x}^{\;}}＞\frac{{R}_{x}^{\;}}{{R}_{A}^{\;}}$时，电流表应用外接法，满足$\frac{{R}_{V}^{\;}}{{R}_{x}^{\;}}＜\frac{{R}_{x}^{\;}}{{R}_{A}^{\;}}$时电流表应用内接法．
字词句篇与同步作文达标系列答案
走进文言文系列答案
阴极射线示波管的聚焦电场是由电极A1、A2形成，实线为电场线，虚线为等势线，Z轴为该电场的中心轴线，P、Q、R为一个从左侧进入聚焦电场的电子运动轨迹上的三点，不计电子的重力，则（ ）| A． | 电极A1的电势高于电极A2的电势 | |
| B． | 电子在P点处的动能小于在Q点处的动能 | |
| C． | 电场中Q点的电场强度小于R点的电场强度 | |
| D． | 电子从P至R的运动过程中，电场力对它一直做正功 |
| A． | 两条磁感线可以相交 | B． | 沿磁感线方向，磁场越来越弱 | ||
| C． | 磁感线总是从N极出发，到S极终止 | D． | 磁感线的疏密程度反映磁场的强弱 |
真空中有两个带同种等量正点电荷q1和q2，a、b为q1、q2连线上的两点，a为连线的中点，c、d为q1、q2连线中垂线上的两点，如图所示，则a、b、c、d四点的电场强度和电势，下列说法正确的是（ ）| A． | a点电势为零 | B． | a点场强大于b点场强 | ||
| C． | c点场强可能小于d点场强 | D． | c点电势可能小于d点电势 |
| A． | E=$\frac{F}{q}$和E=$\frac{kQ}{{r}^{2}}$，都只适用于点电荷产生的电场 | |
| B． | E=$\frac{F}{q}$适用于任何电场，E=$\frac{kQ}{{r}^{2}}$只适用于点电荷产生的电场 | |
| C． | E=$\frac{F}{q}$只适用于点电荷产生的电场，E=$\frac{kQ}{{r}^{2}}$适用于任何电场 | |
| D． | E=$\frac{F}{q}$和E=$\frac{kQ}{{r}^{2}}$ 都适用于任何电场 |
如图所示，甲车质量m1=20kg，车上有质量M=50kg的人，甲车（连同车上的人）以v=3m/s的速度向右滑行．此时质量m2=50kg的乙车正以v0=1.8m/s的速度迎面滑来，为了避免两车相撞，当两车相距适当距离时，人从甲车跳到乙车上，求人跳出甲车的水平速度（相对地面）应当在什么范围内才能避免两车相撞？（不计地面和小车间的摩擦，设乙车足够长，取g=10m/s2）
如图甲所示，A、B两球完全相同，质量均为m，用两根等长的细线悬挂在O点，两球之间固连着一根劲度系数为k的轻弹簧，静止不动时，弹簧位于水平方向，两根细线之间的夹角为2θ，已知下列各情况中弹簧与AB两球心连线始终共线，重力加速度为g．求：