题目内容
3.小河宽为 d,河水中各点水流速度大小与各点到较近河岸边的距离成正比,v水=kx,k=$\frac{4{v}_{0}}{d}$,x是各点到近岸的距离,小船划水速度为v0,若要使船以最短时间渡河,则下列说法中正确的是( )| A. | 船在行驶过程中,船头始终与河岸垂直 | |
| B. | 船在河水中航行的轨迹是一条直线 | |
| C. | 船渡河的最短时间是$\frac{d}{{v}_{0}}$ | |
| D. | 小船在行驶过程中最大速度为$\sqrt{17}$v0 |
分析 将小船的运动分解为沿船头指向和顺水流方向的两个分运动,两个分运动同时发生,互不干扰,与合运动相等效.根据运动的合成来确定初速度与加速度的方向关系,从而确定来小船的运动轨迹;小船垂直河岸渡河时间最短,由位移与速度的比值来确定运动的时间;由水流速度的大小与各点到较近河岸边的距离成正比,来确定水流的速度,再由小船在静水中的运动速度,从而确定小船的渡河速度.
解答 解:AC、将小船的运动分解为沿船头指向和顺水流方向的两个分运动,两个分运动同时发生,互不干扰,故渡河时间与顺水流方向的分运动无关,当船头与河岸垂直时,沿船头方向的分运动的分位移最小,故渡河时间最短,最短时间为$\frac{d}{{v}_{0}}$,故AC正确,
B、小船的速度为沿船头指向和顺水流方向的两个分运动的分速度的矢量和,而两个分速度垂直,故当顺水流方向的分速度最大时,合速度最大,合速度的方向随顺水流方向的分速度的变化而变化,故小船到达河中心时速度最大,且运动轨迹为曲线,故B错误;
D、小船到达离河对岸$\frac{d}{2}$处,则水流速度最大,最大值为v=$\frac{4{v}_{0}}{d}×\frac{d}{2}$=2v0,而小船在静水中的速度为v0,所以船的渡河速度为$\sqrt{5}$v0,故D错误;
故选:AC.
点评 本题关键是当船头与河岸垂直时,渡河时间最短,同时合速度与分速度遵循平行四边形定则,同时注意v=kx公式中的x的含义.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
11.在粗糙的水平面上,质量为 m 的物体,在水平恒力 F 的作用下,由静止开始运动,经时间 t 后,速度为 v,如果要使物体的速度增加到 2v,可采用的方法是( )
| A. | 将物体的质量减小为原来的一半,其他条件不变 | |
| B. | 将水平恒力增加到 2F,其他条件不变 | |
| C. | 将时间增加到 2t,其他条件不变 | |
| D. | 将物体质量,水平恒力和时间都增加到原来的 2 倍 |
18.如图甲所示为电场中的一条电场线,在电场线上建立坐标轴,则坐标轴上O~x2间各点的电势分布如图乙所示,则( )


| A. | 在O~x2间,场强先减小后增大 | |
| B. | 在O~x2间,场强方向一定发生了变化 | |
| C. | 若一负电荷从O点运动到x2点,电势能逐渐减小 | |
| D. | 从O点静止释放一仅受电场力作用的正电荷,则该电荷在O~x2间一直做加速运动 |
15.下列说法正确的是( )
| A. | 狭义相对论的长度变化公式为:l=l0$\sqrt{1-(\frac{u}{c})^{2}}$ | |
| B. | 1pF=10-6C/V | |
| C. | 物体做受迫振动时,振动周期由物体的固有周期决定 | |
| D. | 传感器通常是把被测的电信息,按一定的规律转化为与之对应的非电信息的器件 |
12.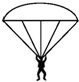 跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞的重力为G2,有8根相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上,如图所示(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角.那么每根拉线上的张力大小为( )
跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞的重力为G2,有8根相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上,如图所示(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角.那么每根拉线上的张力大小为( )
 跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞的重力为G2,有8根相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上,如图所示(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角.那么每根拉线上的张力大小为( )
跳伞运动员打开伞后经过一段时间,将在空中保持匀速降落.已知运动员和他身上装备的总重力为G1,圆顶形降落伞的重力为G2,有8根相同的拉线,一端与飞行员相连(拉线重力不计),另一端均匀分布在伞面边缘上,如图所示(图中没有把拉线都画出来),每根拉线和竖直方向都成30°角.那么每根拉线上的张力大小为( )| A. | $\frac{{\sqrt{3}({G_1}+{G_2})}}{12}$ | B. | $\frac{{\sqrt{3}{G_1}}}{12}$ | C. | $\frac{{{G_1}+{G_2}}}{8}$ | D. | $\frac{G_1}{4}$ |
13. 如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升.若小车以v1的速度匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为T,则下列关系式正确的是( )
如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升.若小车以v1的速度匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为T,则下列关系式正确的是( )
 如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升.若小车以v1的速度匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为T,则下列关系式正确的是( )
如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升.若小车以v1的速度匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为T,则下列关系式正确的是( )| A. | v2=v1cosθ | B. | v2cosθ=v1 | C. | T=mg | D. | T>mg |
 如图所示,滑块A的质量为m,小车B的质量为M,且M=2m,滑块与小车平板之间的动摩擦因数为μ.小车一开始静止,滑块以速度v0滑上小车,并最终停在小车上.滑块在平板小车上滑行1s后相对小车静止.求:
如图所示,滑块A的质量为m,小车B的质量为M,且M=2m,滑块与小车平板之间的动摩擦因数为μ.小车一开始静止,滑块以速度v0滑上小车,并最终停在小车上.滑块在平板小车上滑行1s后相对小车静止.求: