题目内容
11. 如图所示,平行于纸面向右的匀强磁场的磁感应强度为B1=1T.长l=1m的直导线中通有I=1A的恒定电流,导线平行于纸面与B1成60°角时,发现其受安培力为0;而将导线垂直纸面放入时,可测其受安培力大小为2N,则该区域同时存在的另一匀强磁场的磁感应强度B2大小可能为( )
如图所示,平行于纸面向右的匀强磁场的磁感应强度为B1=1T.长l=1m的直导线中通有I=1A的恒定电流,导线平行于纸面与B1成60°角时,发现其受安培力为0;而将导线垂直纸面放入时,可测其受安培力大小为2N,则该区域同时存在的另一匀强磁场的磁感应强度B2大小可能为( )| A. | 1T | B. | $\sqrt{3}$T | C. | 2T | D. | $\sqrt{7}$T |
分析 “导线平行于纸面与B1成60°的夹角时,发现其不受安培力”,根据左手定则可知,合磁场一定与电流方形平行,可能相同,也可能相反.因此,将导线垂直于纸面放置时,所受的安培力的合力一定跟导线垂直,可能垂直向上,也可能垂直向下.根据这两种情况分别计算.
解答 解:根据题意“导线平行于纸面与B1成60°的夹角时,发现其不受安培力”
说明合磁场一定与电流方向平行,即合磁场可能跟电流方向相同,或相反.
根据左手定则,将导线垂直于纸面放置时,所受的安培力的合力一定跟导线垂直.
垂直放置时,不妨设电流方向垂直纸面向内,则两种情况分别如下图.
B1产生的安培力为F1,方向垂直B1向下,大小为F1=B1IL=1N.
第一种情况,合磁场跟电流方向相同.
根据平行四边形定则,以F1为邻边、F合为对角线作另一个邻边F2,如上图所示.
根据几何关系可知α=30°,
又F合=2N、F1=1N,所以F2=$\sqrt{3}$.
F2=B2IL,${B}_{2}=\frac{{F}_{2}}{IL}=\sqrt{3}T$,
如图,B2的方向在纸面内垂直B1向上.
第二种情况,合磁场跟电流方向相反.
根据平行四边形定则,以F1为邻边、F合′为对角线作另一个邻边F2′,如下图所示.
如图,θ=30°,所以根据余弦定理,有
$F{′}_{2}=\sqrt{{F}_{1}^{2}{+F}_{合}^{′2}-2{F}_{1}{F}_{合}′cos(90°+θ)}$=$\sqrt{7}$N.
F2′=B2′IL,$B{′}_{2}=\frac{F{′}_{2}}{IL}=\sqrt{7}T$,
故选:BD
点评 磁感应强度是矢量,矢量的合成与分解满足平行四边形定则,同时要注意安培力与磁场方向是垂直的.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
2. 水平光滑的平行导轨MN、PQ上放着光滑导体棒ab、cd,两棒用绝缘细线系住,开始时匀强磁场的方向如图甲所示,而磁感应强度B随时间t的变化如图乙所示,不计ab、cd间电流的相互作用,则细线中的张力( )
水平光滑的平行导轨MN、PQ上放着光滑导体棒ab、cd,两棒用绝缘细线系住,开始时匀强磁场的方向如图甲所示,而磁感应强度B随时间t的变化如图乙所示,不计ab、cd间电流的相互作用,则细线中的张力( )
 水平光滑的平行导轨MN、PQ上放着光滑导体棒ab、cd,两棒用绝缘细线系住,开始时匀强磁场的方向如图甲所示,而磁感应强度B随时间t的变化如图乙所示,不计ab、cd间电流的相互作用,则细线中的张力( )
水平光滑的平行导轨MN、PQ上放着光滑导体棒ab、cd,两棒用绝缘细线系住,开始时匀强磁场的方向如图甲所示,而磁感应强度B随时间t的变化如图乙所示,不计ab、cd间电流的相互作用,则细线中的张力( )| A. | 在0到t0时间内逐渐增大 | B. | 在0到t0时间内逐渐减小 | ||
| C. | 在0到t0时间内不变 | D. | 在t0到t1时间内为零 |
6.质量为m的带正电小球由空中A点无初速度自由下落,在t秒末加上竖直向上、范围足够大的匀强电场,再经过2t秒小球又回到A点.不计空气阻力且小球从未落地,则( )
| A. | 整个过程中小球机械能增加了$\frac{9}{8}$mg2t2 | |
| B. | 从加电场开始到小球运动到最低点的时间为$\frac{2}{3}$t | |
| C. | 从加电场开始到小球运动到最高点时小球动能变化了$\frac{5}{8}$mg2t2 | |
| D. | 从最低点到A点小球重力势能变化了$\frac{3}{5}$mg2t2 |
20.一个带正电的质点,电量q=2.0×10-9C,在静电场中由a点移到b点,在这个过程中,除电场力外,其他力做的功为6.0×10-5J,质点的动能增加了8.0×10-5J,则A、B两点间的电势差Uab为( )
| A. | 1.0×104V | B. | 3.0×104V | C. | 4.0×104V | D. | 7.0×104V |
1. 质量为m的小球(视为质点)从某液面上方一定高度处由静止释放,进入液体后受到的阻力与其速率成正比,小球在整个运动过程中的速率随时间变化的规律如图所示,取重力加速度为g.则下列分析中正确的是( )
质量为m的小球(视为质点)从某液面上方一定高度处由静止释放,进入液体后受到的阻力与其速率成正比,小球在整个运动过程中的速率随时间变化的规律如图所示,取重力加速度为g.则下列分析中正确的是( )
 质量为m的小球(视为质点)从某液面上方一定高度处由静止释放,进入液体后受到的阻力与其速率成正比,小球在整个运动过程中的速率随时间变化的规律如图所示,取重力加速度为g.则下列分析中正确的是( )
质量为m的小球(视为质点)从某液面上方一定高度处由静止释放,进入液体后受到的阻力与其速率成正比,小球在整个运动过程中的速率随时间变化的规律如图所示,取重力加速度为g.则下列分析中正确的是( )| A. | 小球在液体中先做匀减速运动后做匀速运动 | |
| B. | 小球在液体中受到的阻力与其速率的比值为$\frac{mg}{{v}_{1}}$ | |
| C. | 小球进入液体瞬间的加速度大小为$\frac{{v}_{1}-{v}_{2}}{{v}_{2}}$g | |
| D. | 小球在t1~t2时间内的平均速度大于$\frac{{v}_{1}+{v}_{2}}{2}$ |
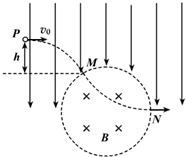 某空间存在一竖直向下的匀强电场和圆形区域的匀强磁场,磁感应强度为B,方向垂直纸面向里,如图所示.一质量为m,带电量为+q的粒子,从P点以水平速度v0射入电场中,然后从M点射入磁场,从N点射出磁场.已知,带电粒子从M点射入磁场时,速度与竖直方向成30°角,弧MN是圆周长的$\frac{1}{3}$,粒子重力不计.求:
某空间存在一竖直向下的匀强电场和圆形区域的匀强磁场,磁感应强度为B,方向垂直纸面向里,如图所示.一质量为m,带电量为+q的粒子,从P点以水平速度v0射入电场中,然后从M点射入磁场,从N点射出磁场.已知,带电粒子从M点射入磁场时,速度与竖直方向成30°角,弧MN是圆周长的$\frac{1}{3}$,粒子重力不计.求: 如图所示,在坐标系的第一、四象限存在一宽度为a、垂直纸面向外的有界匀强磁场,磁感应强度的大小为B;在第三象限存在与y轴正方向成θ=60°角的匀强电场.一个粒子源能释放质量为m、电荷量为+q的粒子,粒子的初速度可以忽略.粒子源在点P(-$\frac{\sqrt{3}}{2}$a,-$\frac{1}{2}$a)时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出.不计粒子的重力及粒子间相互作用力.求:
如图所示,在坐标系的第一、四象限存在一宽度为a、垂直纸面向外的有界匀强磁场,磁感应强度的大小为B;在第三象限存在与y轴正方向成θ=60°角的匀强电场.一个粒子源能释放质量为m、电荷量为+q的粒子,粒子的初速度可以忽略.粒子源在点P(-$\frac{\sqrt{3}}{2}$a,-$\frac{1}{2}$a)时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出.不计粒子的重力及粒子间相互作用力.求: 甲同学用20分度的游标卡尺测电阻丝的直径时,主尺的第18条刻度线与游标的第18条刻度线对齐(计数时不含零刻度线),则甲同学测量的电阻丝的直径为0.90mm;乙同学用千分尺测量电阻丝的直径时如图所示,乙同学的测量值为0.700±0.001mm.你认为甲乙两同学测量结果不一致的原因是:系统误差.
甲同学用20分度的游标卡尺测电阻丝的直径时,主尺的第18条刻度线与游标的第18条刻度线对齐(计数时不含零刻度线),则甲同学测量的电阻丝的直径为0.90mm;乙同学用千分尺测量电阻丝的直径时如图所示,乙同学的测量值为0.700±0.001mm.你认为甲乙两同学测量结果不一致的原因是:系统误差. 某司机乙驾驶一辆卡车正以一定速度在平直公路上匀速行驶.经过图甲所示的限速牌标志为40km/h的位置时,突然发现离他25.5m处停着一辆正在维修的小轿车,于是该司机采取了紧急刹车措施,使卡车做匀减速直线运动,结果还是与小轿车发生碰撞.在处理事故时,交警甲用图乙所示的测定反应时间的方法对司机乙进行了测试,发现他握住木尺时,木尺已经自由下降了20cm.(g取10m/s2)已知这种卡车急刹车时产生的加速度大小为5m/s2.
某司机乙驾驶一辆卡车正以一定速度在平直公路上匀速行驶.经过图甲所示的限速牌标志为40km/h的位置时,突然发现离他25.5m处停着一辆正在维修的小轿车,于是该司机采取了紧急刹车措施,使卡车做匀减速直线运动,结果还是与小轿车发生碰撞.在处理事故时,交警甲用图乙所示的测定反应时间的方法对司机乙进行了测试,发现他握住木尺时,木尺已经自由下降了20cm.(g取10m/s2)已知这种卡车急刹车时产生的加速度大小为5m/s2.