题目内容
16.假设宇航员乘坐宇宙飞船到某行星科学考擦,当宇宙飞船在靠近该行星表面做匀速圆周运送时,测得环绕周期为T,已知该行星的半径为R,引力常量为G.求:(1)该星球表面重力加速度;
(2)该行星的密度.
分析 (1)飞船绕星球做圆周运动,万有引力提供向心力,应用牛顿第二定律求出重力加速度.
(2)应用牛顿第二定律求出行星的质量,然后求出行星的密度.
解答 解:(1)飞船绕行星做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$(\frac{2π}{T})^{2}$R,
星球表面的物体受到的重力等于万有引力,即:G$\frac{Mm′}{{R}^{2}}$=m′g,
解得:g=$\frac{4{π}^{2}R}{{T}^{2}}$;
(2)飞船绕行星做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$(\frac{2π}{T})^{2}$R,
行星的密度:ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$,
解得:ρ=$\frac{3π}{G{T}^{2}}$;
答:(1)该星球表面重力加速度为$\frac{4{π}^{2}R}{{T}^{2}}$;
(2)该行星的密度为$\frac{3π}{G{T}^{2}}$.
点评 本题考查了万有引力定律的应用,考查了求重力加速度与行星密度问题,知道万有引力提供飞船做圆周运动的向心力是解题的关键,应用万有引力公式、牛顿第二定律与密度公式可以解题.

练习册系列答案
相关题目
7.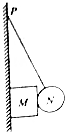 如图所示,光滑小球N用轻绳系在竖直墙壁上的P点,在球N和墙壁之间夹有一长方体物块M,系统处于静止状态.现用拇指将绳按在墙上从P点沿墙缓慢下移少许,则在缓慢下移过程中( )
如图所示,光滑小球N用轻绳系在竖直墙壁上的P点,在球N和墙壁之间夹有一长方体物块M,系统处于静止状态.现用拇指将绳按在墙上从P点沿墙缓慢下移少许,则在缓慢下移过程中( )
 如图所示,光滑小球N用轻绳系在竖直墙壁上的P点,在球N和墙壁之间夹有一长方体物块M,系统处于静止状态.现用拇指将绳按在墙上从P点沿墙缓慢下移少许,则在缓慢下移过程中( )
如图所示,光滑小球N用轻绳系在竖直墙壁上的P点,在球N和墙壁之间夹有一长方体物块M,系统处于静止状态.现用拇指将绳按在墙上从P点沿墙缓慢下移少许,则在缓慢下移过程中( )| A. | 细绳对球N的拉力逐渐变大 | B. | 物块M受到墙壁的弹力逐渐增大 | ||
| C. | 物块M受到墙壁的摩擦力大小不变 | D. | 物块M可能沿墙下滑 |
11. 城市的路灯、无轨电车的供电线路等,经常用三角形的支架悬挂,如图所示为这类结构的简化模型,硬杆OB左端可绕通过B点且垂直于纸面的轴无摩擦的转动,钢索OA与硬杆右端O点相连,上端固定于A点,钢索OA和硬杆所受的重力均可忽略,现将一质量不变的重物悬挂于O点,硬杆OB水平,若保持钢索的悬挂点A位置不变,将钢索缓慢变短使OB杆绕B端转动,则在上述变化过程中,下列说法中正确的是( )
城市的路灯、无轨电车的供电线路等,经常用三角形的支架悬挂,如图所示为这类结构的简化模型,硬杆OB左端可绕通过B点且垂直于纸面的轴无摩擦的转动,钢索OA与硬杆右端O点相连,上端固定于A点,钢索OA和硬杆所受的重力均可忽略,现将一质量不变的重物悬挂于O点,硬杆OB水平,若保持钢索的悬挂点A位置不变,将钢索缓慢变短使OB杆绕B端转动,则在上述变化过程中,下列说法中正确的是( )
 城市的路灯、无轨电车的供电线路等,经常用三角形的支架悬挂,如图所示为这类结构的简化模型,硬杆OB左端可绕通过B点且垂直于纸面的轴无摩擦的转动,钢索OA与硬杆右端O点相连,上端固定于A点,钢索OA和硬杆所受的重力均可忽略,现将一质量不变的重物悬挂于O点,硬杆OB水平,若保持钢索的悬挂点A位置不变,将钢索缓慢变短使OB杆绕B端转动,则在上述变化过程中,下列说法中正确的是( )
城市的路灯、无轨电车的供电线路等,经常用三角形的支架悬挂,如图所示为这类结构的简化模型,硬杆OB左端可绕通过B点且垂直于纸面的轴无摩擦的转动,钢索OA与硬杆右端O点相连,上端固定于A点,钢索OA和硬杆所受的重力均可忽略,现将一质量不变的重物悬挂于O点,硬杆OB水平,若保持钢索的悬挂点A位置不变,将钢索缓慢变短使OB杆绕B端转动,则在上述变化过程中,下列说法中正确的是( )| A. | 钢索对O点的拉力变大 | B. | 硬杆对O点的支持力变小 | ||
| C. | 硬杆对O点的支持力不变 | D. | 钢索对O点的拉力不变 |
1. 如图所示,某人站在距水平地面高h处的山顶用球拍水平击出一个质量为m的小球(不计空气阻力),球刚好落在图中L处的A点,则下列说法正确的是( )
如图所示,某人站在距水平地面高h处的山顶用球拍水平击出一个质量为m的小球(不计空气阻力),球刚好落在图中L处的A点,则下列说法正确的是( )
 如图所示,某人站在距水平地面高h处的山顶用球拍水平击出一个质量为m的小球(不计空气阻力),球刚好落在图中L处的A点,则下列说法正确的是( )
如图所示,某人站在距水平地面高h处的山顶用球拍水平击出一个质量为m的小球(不计空气阻力),球刚好落在图中L处的A点,则下列说法正确的是( )| A. | 球被击出后在水平方向做匀加速直线运动 | |
| B. | 该球从被击出到落至A点所用的时间仅由L决足 | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2h}{g}}$ | |
| D. | 击球时球拍对球做的功为$\frac{mg{L}^{2}}{4h}$ |
8. 如图所示,在水平地面上向左做匀速直线运动的汽车,通过定滑轮用绳子吊起一质量为m的重物,若小车和被吊重物在同一时刻的速率分别为v1和v2,绳子对重物的拉力为T,已知重力的加速度为g,比较v1和v2,T与mg大小关系,下列判断正确的是( )
如图所示,在水平地面上向左做匀速直线运动的汽车,通过定滑轮用绳子吊起一质量为m的重物,若小车和被吊重物在同一时刻的速率分别为v1和v2,绳子对重物的拉力为T,已知重力的加速度为g,比较v1和v2,T与mg大小关系,下列判断正确的是( )
 如图所示,在水平地面上向左做匀速直线运动的汽车,通过定滑轮用绳子吊起一质量为m的重物,若小车和被吊重物在同一时刻的速率分别为v1和v2,绳子对重物的拉力为T,已知重力的加速度为g,比较v1和v2,T与mg大小关系,下列判断正确的是( )
如图所示,在水平地面上向左做匀速直线运动的汽车,通过定滑轮用绳子吊起一质量为m的重物,若小车和被吊重物在同一时刻的速率分别为v1和v2,绳子对重物的拉力为T,已知重力的加速度为g,比较v1和v2,T与mg大小关系,下列判断正确的是( )| A. | v1=v2,T=mg | B. | v1>v2,T=mg | C. | v1<v2,T<mg | D. | v1>v2,T>mg |
5.某屋顶为半球形,一人在屋顶上向上缓慢爬行(如图所示),则他在向上爬的过程中( ) 

| A. | 屋顶对他的摩擦力变大 | B. | 屋顶对他的摩擦力不变 | ||
| C. | 屋顶对他的支持力变大 | D. | 屋顶对他的支持力不变 |
6. 某电视台娱乐节目进行了一项抛球入框游戏,如图所示,该游戏球框(框壁厚忽略不计)紧靠竖直墙壁放在水平地面上.球框高度和球框左侧壁离墙壁的距离均为L.某同学将球(可视为质点)正对竖直墙壁水平抛出并投入框中,球的抛出点离地面的高度H=3L,离墙壁的水平距离d=5L.球与墙壁碰撞前后瞬间速度大小相等,方向关于墙壁对称,不计与墙和框壁碰撞的时间.已知球的质量为m,重力加速度为g,空气阻力不计.则下列说法正确的是( )
某电视台娱乐节目进行了一项抛球入框游戏,如图所示,该游戏球框(框壁厚忽略不计)紧靠竖直墙壁放在水平地面上.球框高度和球框左侧壁离墙壁的距离均为L.某同学将球(可视为质点)正对竖直墙壁水平抛出并投入框中,球的抛出点离地面的高度H=3L,离墙壁的水平距离d=5L.球与墙壁碰撞前后瞬间速度大小相等,方向关于墙壁对称,不计与墙和框壁碰撞的时间.已知球的质量为m,重力加速度为g,空气阻力不计.则下列说法正确的是( )
 某电视台娱乐节目进行了一项抛球入框游戏,如图所示,该游戏球框(框壁厚忽略不计)紧靠竖直墙壁放在水平地面上.球框高度和球框左侧壁离墙壁的距离均为L.某同学将球(可视为质点)正对竖直墙壁水平抛出并投入框中,球的抛出点离地面的高度H=3L,离墙壁的水平距离d=5L.球与墙壁碰撞前后瞬间速度大小相等,方向关于墙壁对称,不计与墙和框壁碰撞的时间.已知球的质量为m,重力加速度为g,空气阻力不计.则下列说法正确的是( )
某电视台娱乐节目进行了一项抛球入框游戏,如图所示,该游戏球框(框壁厚忽略不计)紧靠竖直墙壁放在水平地面上.球框高度和球框左侧壁离墙壁的距离均为L.某同学将球(可视为质点)正对竖直墙壁水平抛出并投入框中,球的抛出点离地面的高度H=3L,离墙壁的水平距离d=5L.球与墙壁碰撞前后瞬间速度大小相等,方向关于墙壁对称,不计与墙和框壁碰撞的时间.已知球的质量为m,重力加速度为g,空气阻力不计.则下列说法正确的是( )| A. | 不论以多大的速度水平抛出,只要能投入框中,落到框底所用时间相同 | |
| B. | 为使球落入框中,球抛出时的最小速度为$\sqrt{gL}$ | |
| C. | 球刚落到框底时的最小动能为5mgL | |
| D. | 为使球落入框中,球与墙壁碰撞的最高点离地面的高度应为$\frac{29}{18}$L |