题目内容
16.万有引力定律的表达式为:F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,其中G为引力常量.把它应用于太阳-行星系统,已知地球绕太阳公转的半径为R,周期为T,则由此可以求出( )| A. | 地球的质量 | B. | 地球的密度 | C. | 太阳的质量 | D. | 太阳的态度 |
分析 研究行星绕太阳做匀速圆周运动,根据万有引力提供向心力,列出等式可求出太阳的质量
解答 解:设太阳的质量为M,地球的质量为m.地球绕太阳做圆周运动的向心力由太阳的万有引力提供,则有:
$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$
得$M=\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}}$,已知r和T,可求出太阳的质量M,但不能求出地球的质量m和地球的密度.
由于太阳的半径未知,也不能求出太阳的密度.
故选:C
点评 已知环绕天体的公转半径和周期,根据万有引力提供向心力,列出等式只能求出中心体的质量.要求出行星的质量,我们可以在行星周围找一颗卫星研究,即把行星当成中心体

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.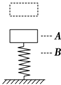 一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )
一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )
 一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )
一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )| A. | 物块从A处下降到B处的过程中,速率不断减小 | |
| B. | 物块从B处上升到A处的过程中,速率不断增大 | |
| C. | 物块在B处时,所受合力为零 | |
| D. | 物块从A处下降到B处的过程中速率先增大,后减小 |
11.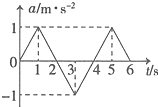 一质点以v0=5m/s的初速度从t=0时刻开始做直线运动,其加速度随时t变化的图
一质点以v0=5m/s的初速度从t=0时刻开始做直线运动,其加速度随时t变化的图
象如图所示,则下列说法正确的是( )
 一质点以v0=5m/s的初速度从t=0时刻开始做直线运动,其加速度随时t变化的图
一质点以v0=5m/s的初速度从t=0时刻开始做直线运动,其加速度随时t变化的图象如图所示,则下列说法正确的是( )
| A. | 第1s末质点的速度为6m/s | B. | 运动过程中质点的最大速度为6m/s | ||
| C. | 第ls内质点的位移为5.25m | D. | 4s末质点回到t=0时刻的位置 |
1. 如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其速度为( )
如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其速度为( )
 如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其速度为( )
如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其速度为( )| A. | 2$\sqrt{\frac{g(h+x)}{3}}$ | B. | 2$\sqrt{g(h+x)}$ | C. | 2$\sqrt{gh}$ | D. | 2$\sqrt{\frac{gh}{3}}$ |
8.如图所示,可看成质点的a、b、c是在地球大气层外圆轨道上运动的3颗卫星,下列说法正确的是( )


| A. | b、c的线速度大小相等,且大于a的线速度 | |
| B. | b、c的向心加速度大小相等,且小于a的向心加速度 | |
| C. | b、c的角速度大小相等,且大于a的角速度 | |
| D. | c只要加速就可以追上b |
 如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出.则该玻璃棒的折射率为$\sqrt{2}$,若将入射光向N端平移,当第一次射到弧面EF上时能(填“能”、“不能”或“无法确定能否”)发生全反射.
如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出.则该玻璃棒的折射率为$\sqrt{2}$,若将入射光向N端平移,当第一次射到弧面EF上时能(填“能”、“不能”或“无法确定能否”)发生全反射.
 我质量为4kg的木块放在倾角为30°长为15m的固定斜面上时,木块恰好能沿斜面匀速下滑,若改用沿斜面向上的恒力F拉木块,木块从静止开始沿斜面运动2.5m所用的时间为1s(g取10m/s2)求:
我质量为4kg的木块放在倾角为30°长为15m的固定斜面上时,木块恰好能沿斜面匀速下滑,若改用沿斜面向上的恒力F拉木块,木块从静止开始沿斜面运动2.5m所用的时间为1s(g取10m/s2)求: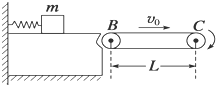 如图所示,质量为m的滑块,放在光滑的水平平台上,平台右端B与水平传送带相接,传送带的运行速度为v0,长为L.今将滑块缓慢向左压缩固定在平台上的轻弹簧,到达某处时突然释放.当滑块滑到传送带右端C时,恰好与传送带速度相同.滑块与传送带间的动摩擦因数为μ.
如图所示,质量为m的滑块,放在光滑的水平平台上,平台右端B与水平传送带相接,传送带的运行速度为v0,长为L.今将滑块缓慢向左压缩固定在平台上的轻弹簧,到达某处时突然释放.当滑块滑到传送带右端C时,恰好与传送带速度相同.滑块与传送带间的动摩擦因数为μ.